Úloha 14
| zobraz celé řešení | |
| << předchozí snímek | následující snímek>> |
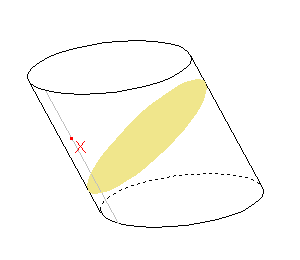 |
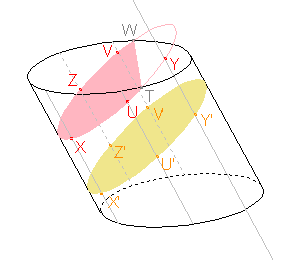
Zadání: Sestrojte řez kosého válce rovinou, která prochází bodem X a je rovnoběžná s danou rovinou, viz obrázek.
K sestrojení elipsy, jejíž část je průsečnicí pláště daného tělesa a roviny řezu, nám stačí pět bodů.
Nejprve si zvolíme pomocné body X', U', Y', V', Z', které leží na průniku dané roviny s pláštěm daného tělesa. K těmto bodům budeme hledat příslušné body X, U, Y, V, Z, které budou ležet na elipse, jejíž část bude průsečnicí pláště daného tělesa a roviny řezu.
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'U', proto jsou průsečnice roviny XX'U' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky.
Můžeme tedy sestrojit rovnoběžku k přímce X'U' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem U'. Sestrojíme tedy bod U, který je průsečíkem rovnoběžky k přímce X'U' procházející bodem X a rovnoběžky k přímce XX' procházející bodem U'.
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'Y', proto jsou průsečnice roviny XX'Y' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky.
Můžeme tedy sestrojit rovnoběžku k přímce X'Y' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem Y'. Sestrojíme tedy bod Y, který je průsečíkem rovnoběžky k přímce X'Y' procházející bodem X a rovnoběžky k přímce XX' procházející bodem Y'.
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'V', proto jsou průsečnice roviny XX'V' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky.
Můžeme tedy sestrojit rovnoběžku k přímce X'V' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem V'. Sestrojíme tedy bod V, který je průsečíkem rovnoběžky k přímce X'V' procházející bodem X a rovnoběžky k přímce XX' procházející bodem V'.
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'Z', proto jsou průsečnice roviny XX'Z' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky.
Můžeme tedy sestrojit rovnoběžku k přímce X'Z' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem Z'. Sestrojíme tedy bod Z, který je průsečíkem rovnoběžky k přímce X'Z' procházející bodem X a rovnoběžky k přímce XX' procházející bodem Z'.
Pomocí bodů X, U, Y, V, Z již můžeme sestrojit elipsu, jejíž část bude průsečnicí pláště daného tělesa a roviny řezu.
Ještě potřebujeme najít hranici řezu v horní podstavě. Touto hranicí je úsečka TW, kde body T, W jsou průsečíky elipsy a horní podstavy.
Nyní známe vše potřebné k sestrojení řezu daného tělesa.
|
zobraz řešení interaktivně
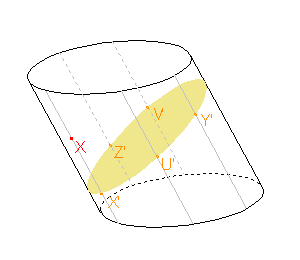 |
K sestrojení elipsy, jejíž část je průsečnicí pláště daného tělesa a roviny řezu, nám stačí pět bodů. Nejprve si zvolíme pomocné body X', U', Y', V', Z', které leží na průniku dané roviny s pláštěm daného tělesa. K těmto bodům budeme hledat příslušné body X, U, Y, V, Z, které budou ležet na elipse, jejíž část bude průsečnicí pláště daného tělesa a roviny řezu. |
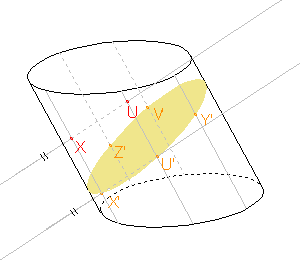 |
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'U', proto jsou průsečnice roviny XX'U' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky. Můžeme tedy sestrojit rovnoběžku k přímce X'U' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem U'. Sestrojíme tedy bod U, který je průsečíkem rovnoběžky k přímce X'U' procházející bodem X a rovnoběžky k přímce XX' procházející bodem U'. |
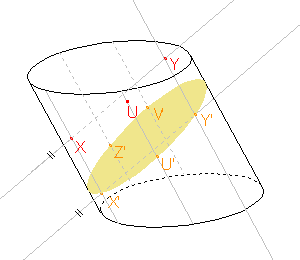 |
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'Y', proto jsou průsečnice roviny XX'Y' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky. Můžeme tedy sestrojit rovnoběžku k přímce X'Y' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem Y'. Sestrojíme tedy bod Y, který je průsečíkem rovnoběžky k přímce X'Y' procházející bodem X a rovnoběžky k přímce XX' procházející bodem Y'. |
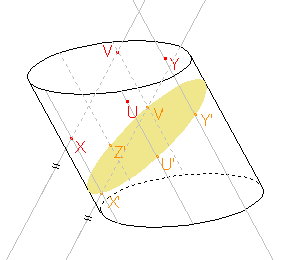 |
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'V', proto jsou průsečnice roviny XX'V' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky. Můžeme tedy sestrojit rovnoběžku k přímce X'V' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem V'. Sestrojíme tedy bod V, který je průsečíkem rovnoběžky k přímce X'V' procházející bodem X a rovnoběžky k přímce XX' procházející bodem V'. |
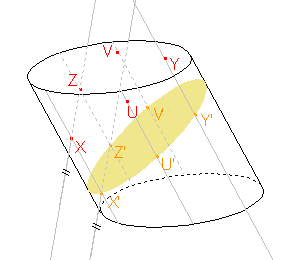 |
Zadaná rovina a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou XX'Z', proto jsou průsečnice roviny XX'Z' se zadanou rovinou a rovinou řezu rovnoběžné. Také tyto roviny vymezují na stranách válce stejně dlouhé úseky. Můžeme tedy sestrojit rovnoběžku k přímce X'Z' procházející bodem X a rovnoběžku k přímce XX', jejíž část je stranou válce a která prochází bodem Z'. Sestrojíme tedy bod Z, který je průsečíkem rovnoběžky k přímce X'Z' procházející bodem X a rovnoběžky k přímce XX' procházející bodem Z'. |
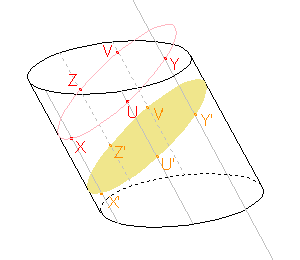 |
Pomocí bodů X, U, Y, V, Z již můžeme sestrojit elipsu, jejíž část bude průsečnicí pláště daného tělesa a roviny řezu. |
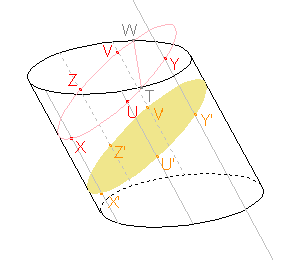 |
Ještě potřebujeme najít hranici řezu v horní podstavě. Touto hranicí je úsečka TW, kde body T, W jsou průsečíky elipsy a horní podstavy. |
 |
Nyní známe vše potřebné k sestrojení řezu daného tělesa. |