Úloha 13
| zobraz celé řešení | |
| << předchozí snímek | následující snímek>> |
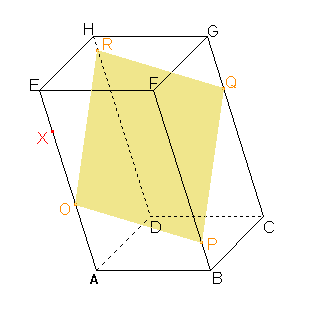 |
Zadání: Sestrojte řez kosého čtyřbokého hranolu rovinou, která je rovnoběžná s rovinou PQR a která prochází bodem X. K řešení této úlohy využijeme stereometrických vět a jejich důsledků.
Sestrojíme bod S a stranu řezu XS v boční stěně ADE dle věty 2 a pozměněného důsledku 2: Rovina PQR a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou boční stěny, proto jsou průsečnice roviny boční stěny s rovinou PQR a rovinou řezu rovnoběžné.
Můžeme tedy sestrojit rovnoběžku ke straně OR procházející bodem X. Průnik rovnoběžky a hrany EH je hledaný bod S a úsečka XS je stranou řezu.
Sestrojíme bod T a stranu řezu XT v přední stěně ABE dle věty 2 a pozměněného důsledku 2: Rovina PQR a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou přední stěny, proto jsou průsečnice roviny přední stěny s rovinou PQR a rovinou řezu rovnoběžné.
Můžeme tedy sestrojit rovnoběžku ke straně OP procházející bodem X. Průnik rovnoběžky a hrany BF je hledaný bod T a úsečka XT je další stranou řezu.
Sestrojíme bod U a stranu řezu TU v boční stěně BCF dle věty 2 a pozměněného důsledku 2: Rovina PQR a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou boční stěny, proto jsou průsečnice roviny boční stěny s rovinou PQR a rovinou řezu rovnoběžné.
Můžeme tedy sestrojit rovnoběžku ke straně PQ procházející bodem T. Průnik rovnoběžky a hrany FG je hledaný bod U a úsečka TU je další stranou řezu.
Dle důsledku 1: Body S, U roviny řezu leží v rovině horní podstavy, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu.
Nyní známe všechny vrcholy a strany mnohoúhelníku, který je řezem daného tělesa.
|
zobraz řešení interaktivně
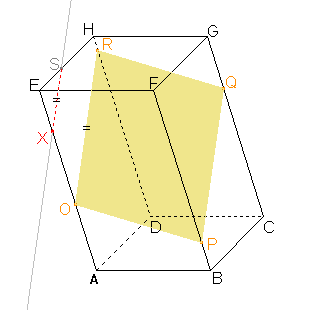 |
Sestrojíme bod S a stranu řezu XS v boční stěně ADE dle věty 2 a pozměněného důsledku 2: Rovina PQR a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou boční stěny, proto jsou průsečnice roviny boční stěny s rovinou PQR a rovinou řezu rovnoběžné. Můžeme tedy sestrojit rovnoběžku ke straně OR procházející bodem X. Průnik rovnoběžky a hrany EH je hledaný bod S a úsečka XS je stranou řezu. |
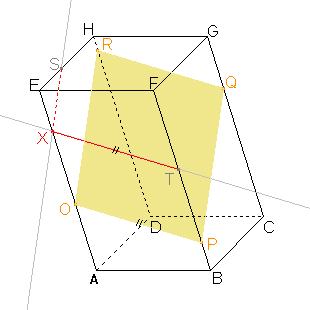 |
Sestrojíme bod T a stranu řezu XT v přední stěně ABE dle věty 2 a pozměněného důsledku 2: Rovina PQR a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou přední stěny, proto jsou průsečnice roviny přední stěny s rovinou PQR a rovinou řezu rovnoběžné. Můžeme tedy sestrojit rovnoběžku ke straně OP procházející bodem X. Průnik rovnoběžky a hrany BF je hledaný bod T a úsečka XT je další stranou řezu. |
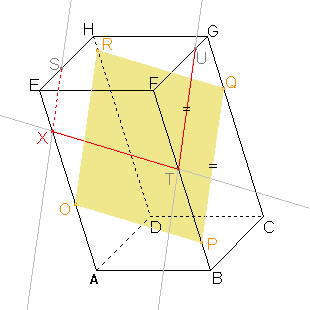 |
Sestrojíme bod U a stranu řezu TU v boční stěně BCF dle věty 2 a pozměněného důsledku 2: Rovina PQR a rovina řezu mají být rovnoběžné a přitom jsou různoběžné s rovinou boční stěny, proto jsou průsečnice roviny boční stěny s rovinou PQR a rovinou řezu rovnoběžné. Můžeme tedy sestrojit rovnoběžku ke straně PQ procházející bodem T. Průnik rovnoběžky a hrany FG je hledaný bod U a úsečka TU je další stranou řezu. |
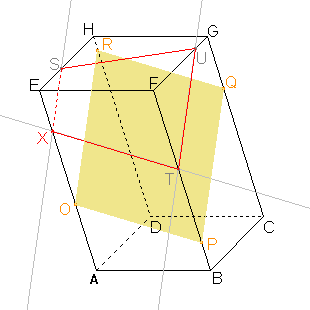 |
Dle důsledku 1: Body S, U roviny řezu leží v rovině horní podstavy, tedy i jejich spojnice leží v rovině této stěny. Průnik spojnice a stěny je další stranou řezu. |
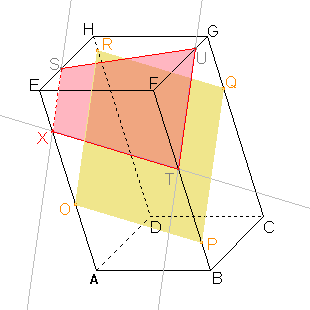 |
Nyní známe všechny vrcholy a strany mnohoúhelníku, který je řezem daného tělesa. |