Ohniskové vlastnosti
Ohniskové vlastnosti paraboly
Touto kapitolou rozšíříme informace z kapitoly Tečny a normály paraboly. Zaměříme se především na vlastnosti ohniska a tečen paraboly.
Pro body souměrně sdružené s ohniskem paraboly platí věta:
Věta P4.1: Všechny body Q souměrně sdružené podle tečen paraboly s ohniskem F leží na řídicí přímce d.
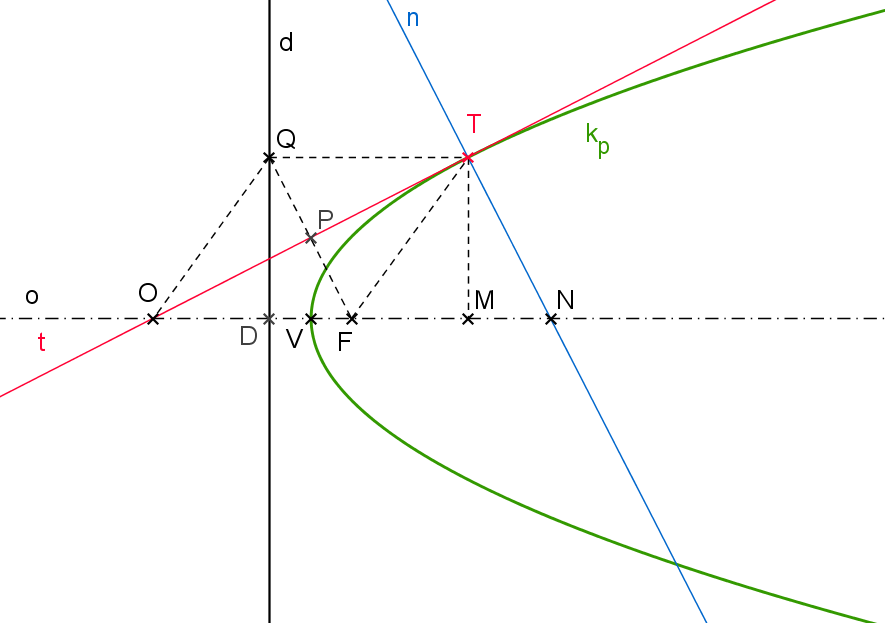
Důkaz: (aplet P4.1) V důkazu se budeme odvolávat na již dokázané, především na větu P3.2.
Zvolme libovolně bod T \in k_p. Sestrojme tečnu t v bodě T. Nechť QT je průvodič bodu T (druhým průvodičem je TF). Polopřímka QT je tím pádem rovnoběžná s osou o (kolmá na d) a bod Q \in d.
Nyní musíme dokázat, že bod Q, který je incidentní s řídicí přímkou, je zároveň souměrně sdružený s ohniskem F podle tečny t.
Nejprve označme P průsečík úsečky FQ s tečnou t. Z definice paraboly se délky průvodičů rovnají, |QT| = |TF|. Podle věty P3.2 jsou úhly PTQ a PTF stejně veliké. Z toho plyne, že trojúhelníky PTF a PTQ jsou shodné podle věty sus. Pokud jsou tedy shodné, potom i délky stran - úseček QP, \, PF se rovnají. Z |QT| = |TF|, \; | \angle PTQ| = | \angle PTF| plyne, že úsečka FQ je kolmá na tečnu t. Bod Q \in d je tedy souměrně sdružený s ohniskem F podle tečny t.
Vlastnost si můžete vyzkoušet v apletu P4.1. Pohybujte tečným bodem T po parabole k_p a sledujte trajektorii bodu Q, který je souměrně sdružený s ohniskem F podle tečny t.
Při konstrukcích může nastat situace, kdy známe tečnu paraboly t, známe i její ohnisko F a řídicí přímku d, přesto nevíme, kde přesně je bod dotyku T tečny a paraboly. Zde využijeme výše zmiňovanou větu P4.1 a najdeme bod Q \in d. Dotykový bod T leží na tečně t a na rovnoběžce s osou o vedené bodem Q.
Tedy: T \in t \cap r, kde r \; || \; o a Q \in r.
Aplet P4.1: Řídicí přímka paraboly a její vrcholová tečna
V apletu P4.1 je také znázorněna vlastnost bodu P, paty kolmice vedené z ohniska F na tečnu t. Při pohybu tečného bodu T po parabole pozorujte trajektorii tohoto bodu. Více napoví následující věta.
Věta P4.2: Paty P všech kolmic sestrojených z ohniska F paraboly na tečny této kuželosečky leží na vrcholové tečně v, která prochází vrcholem V paraboly a je kolmá na její osu o.
Důkaz: (aplet P4.1)
Zvolme libovolně bod T \in k_p, ovšem mimo vrchol V paraboly k_p. Označme bod D jakožto průsečík osy o a řídicí přímky d.
Sestrojme tečnu t v bodě T. K ohnisku F najděme souměrně sdružený bod Q podle tečny t a také patu P kolmice sestrojené z tohoto ohniska na tečnu. Nepochybně platí P \in t \cap QF. Všimněme si pravoúhlého trojúhelníku QDF. Vrchol V je vždy středem strany DF a bod P je středem FQ (věta P4.1). Tudíž spojnice VP je střední příčkou v tomto trojúhelníku. Proto platí VP \, || \, QD. Tedy bod P leží na přímce, která je rovnoběžná s d a prochází vrcholem V. Leží na vrcholové tečně. Pokud bychom dotykový bod T zvolili ve vrcholu V, splynul by s ním i bod P. I pro tento případ by věta P4.1 platila.
V případě, že je dána parabola pomocí F, \, d, \, p a bod T, o kterém ale nevíme, zda-li náleží parabole, použijeme větu P4.3. (čerpána z Kopřivová [8] str.30)
Věta P4.3: Bod T leží na parabole právě tehdy, pokud se kružnice l(T; \, |TF|) dotýká řídicí přímky d.
Věta P4.3 v podstatě popisuje definici kuželosečky. Důkaz je snadný. Je jen potřeba si uvědomit, že bod dotyku kružnice a řídicí přímky je bod Q (bod souměrně sdružený s ohniskem podle tečny v bodě T), tudíž |QT| = |FT|. To nás dovede k definici paraboly.
Popsanou vlastnost si vyzkoušejte v apletu P4.2. Pohybem dotykového bodu T po parabole k_p se mění kružnice l, jež má s řídicí přímkou d jen jeden společný bod, bod Q.
Aplet P4.2: Věta P4.3
Pro konstrukci paraboly jsou užitečné ještě některé další speciální věty, které si postupně ukážeme.
Věta P4.4: Spojnice průsečíku R dvou různých tečen t_1, \, t_2 paraboly a půlicího bodu M tětivy T_1 T_2 jejich bodů dotyku je rovnoběžná se směrem osy o.
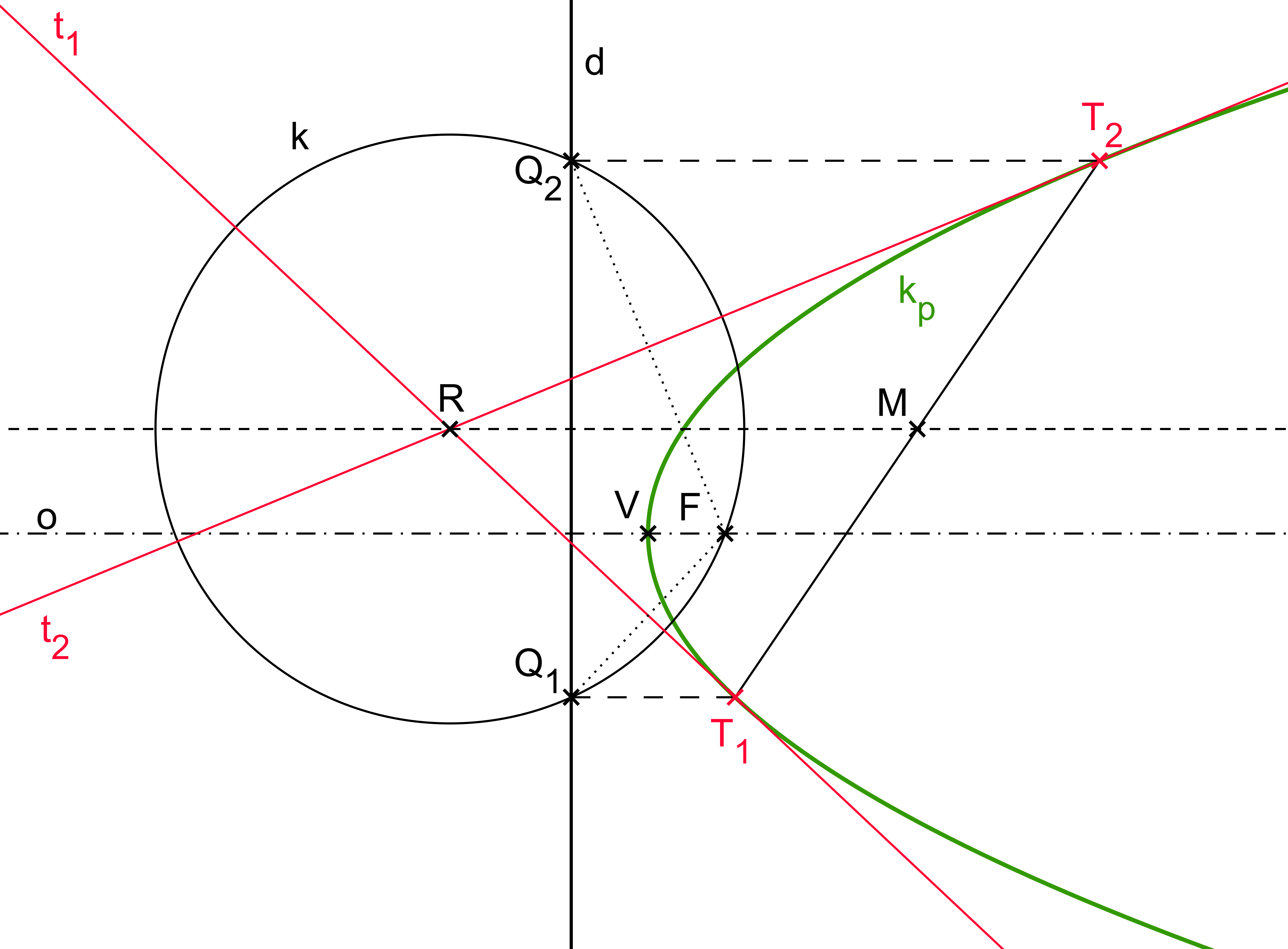
Důkaz: (obrázek P4.1; čerpán z Urban [13] str.52)
Nechť je dána parabola k_p. Zvolme na ní dva různé body T_1, \, T_2 a sestrojme v nich tečny t_1, \, t_2. Jejich průsečík označme R.
Kolmice z bodu R na řídicí přímku d půlí tětivu Q_1Q_2 kružnice k, jež má střed v bodě R a poloměr |RF|. Protože však tato kolmice je rovnoběžná s Q_1T_1 a Q_2T_2 (průvodiče), je tedy rovnoběžná i s osou o a zároveň prochází středem M úsečky T_1T_2. Čímž je věta dokázána.
Obrázek P4.1: Důkaz věty P4.4
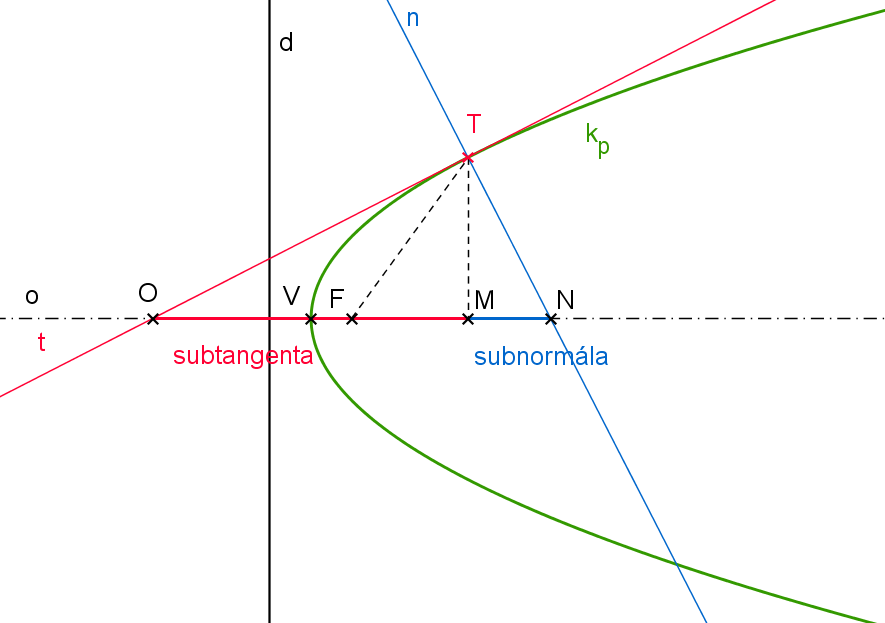
Pro další tři věty budeme potřebovat znát některé nové termíny, které se zde doposud neobjevily. Jde o pojmy subnormála a subtangenta.
První z nich, subnormálou budeme rozumět úsečku MN, kde bod M představuje pravoúhlý průmět dotykového bodu T tečny t paraboly na osu o. Bod N je průsečíkem osy o paraboly a normály n v bodě T (viz obrázek P4.2).
Označíme-li O průsečík tečny t a osy o paraboly, potom subtangentou rozumíme úsečku OM (viz obrázek P4.2).
Oba případy jsou pro tečny, které nejsou vrcholové. Je potřeba si uvědomit, že normála vrcholové tečny je osa o paraboly. A v tomto případě by pojmy subnormála a subtangenta pozbývaly smyslu.
Obrázek P4.2: Subnormála a subtangenta paraboly pro tečnu t
Věta P4.5: Subnormála má konstantní délku rovnou parametru p.
Věta P4.6: Subtangenta je půlena vrcholem V paraboly.
Věta P4.7: Součet subtangenty a subnormály je půlen ohniskem F paraboly.
Důkaz: (obrázek P4.3)
Důkaz předchozích tří vět uvedeme najednou.
Nechť je dána parabola k_p a libovolná tečna t s bodem dotyku T, jež není vrcholová. Zachovejme pojmenování výše uvedených bodů, popř. přímek. Dále označme D, jakožto průsečík d a o, Q \in d bod souměrně sdružený s ohniskem podle tečny t a P \in t patu kolmice z ohniska na tečnu.
Věta P4.5: Podle konstrukce je čtyřúhelník FNTQ rovnoběžník, tedy platí |QF| = |TN|. Pravoúhlé trojúhelníky FDQ a NTM jsou shodné. Odtud již plyne |MN| = |DF| = p.
Věta P4.6: Ve čtyřúhelníku OFTQ jsou úhlopříčky OT a QF k sobě kolmé. Úhlopříčka OT půlí úhlopříčku QF a strany QT, \, OF jsou rovnoběžné. Z toho plyne, že tento čtyřúhelník je buď kosočtverec, nebo čtverec. Odtud platí: |OP| = |PT|. A protože PV \, || \, TM, je |OV| = |VM|, jak jsme měli dokázat.
Z obou předchozích vět snadno odvodíme větu P4.7.
Obrázek P4.3: Důkaz vět P4.5, P4.6, P4.7