Úloha 8
| zobraz celé řešení | |
| << předchozí snímek | následující snímek>> |
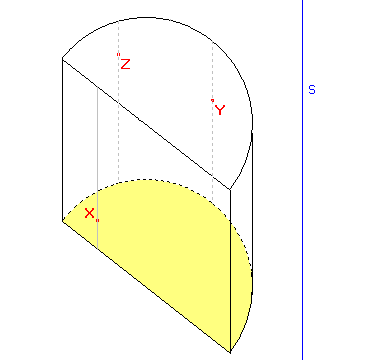 |
Zadání: Sestrojte řez kolmého půlválce rovinou XYZ, kde X, Y, Z jsou body umístěné na plášti půlválce, jak je naznačeno na obrázku. (Půlválec je část válce, která vznikne rozdělením válce rovinou kolmou na podstavu, a která obsahuje osu válce.) Při řešení úlohy využijeme osové afinity mezi rovinou řezu a rovinou dolní podstavy a za směr afinity s vezmeme směr osy válce.
Nejprve musíme najít osu afinity, která je průsečnicí roviny dolní podstavy a roviny řezu dané body XYZ.
K sestrojení osy afinity budeme potřebovat dva body. Jeden bod získáme pomocí bodů X, Z. Obrazem přímky XZ je přímka X'Z', protože obrazem bodu X je bod X' a bodu Z je bod Z'. Průsečíkem přímky XZ a přímky X'Z' je samodružný bod P, který bude ležet na ose afinity.
Druhý bod získáme pomocí bodů X, Y.
Obrazem přímky XY v zadané osové afinitě je přímka X'Y', protože obrazem bodu X je bod X' a bodu Y je bod Y'. Průsečíkem přímky XY a přímky X'Y' je samodružný bod Q, který bude ležet na ose afinity.
Pomocí bodů P, Q již můžeme sestrojit osu afinity o.
K sestrojení elipsy, jejíž část je průsečnicí pláště daného tělesa a roviny řezu, nám stačí pět bodů. Body Y, Z jsou body průsečnice, protože leží na povrchu válce.
Osa afinity leží v rovině dolní podstavy tělesa a protíná hranici podstavy, proto průsečíky T, U osy afinity s hraniční kružnicí dolní podstavy jsou body řezu a současně TU je hranicí řezu.
Další bod získáme pomocí bodů X, X' a V', kde bod X' je obraz bodu X a bod V' zvolíme libovolně na hranici dolní podstavy tělesa.
Bodem V' vedeme rovnoběžku se směrem afinity. Bod R je průsečík přímky X'V' s osou o. Vzorem přímky X'V' je přímka XR a tedy průsečík přímky XR s rovnoběžkou se směrem s v bodě V' je bod elipsy V.
Pátý bod získáme pomocí bodů Y, Y' a W', kde bod Y' je obraz bodu Y a bod W' zvolíme libovolně na hranici dolní podstavy tělesa.
Bodem W' vedeme rovnoběžku se směrem afinity. Bod S je průsečík přímky Y'W' s osou o. Vzorem přímky Y'W' je přímka YS a tedy průsečík přímky YS s rovnoběžkou se směrem s v bodě W' je bod elipsy W.
Pomocí bodů Y, Z, U, V, W již můžeme sestrojit elipsu, jejíž část bude průsečnicí pláště daného tělesa a roviny řezu.
Ještě potřebujeme najít hranici řezu v "přední" stěně. Touto hranicí je úsečka FT, protože body F, T leží ve stejné rovině a bod F je průsečík elipsy a "přední" stěny.
Nyní známe vše potřebné k sestrojení řezu daného tělesa.
|
zobraz řešení interaktivně
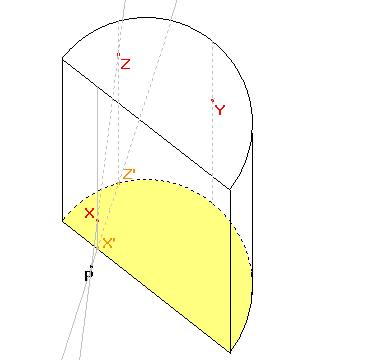 |
Nejprve musíme najít osu afinity, která je průsečnicí roviny dolní podstavy a roviny řezu dané body XYZ. K sestrojení osy afinity budeme potřebovat dva body. Jeden bod získáme pomocí bodů X, Z. Obrazem přímky XZ je přímka X'Z', protože obrazem bodu X je bod X' a bodu Z je bod Z'. Průsečíkem přímky XZ a přímky X'Z' je samodružný bod P, který bude ležet na ose afinity. |
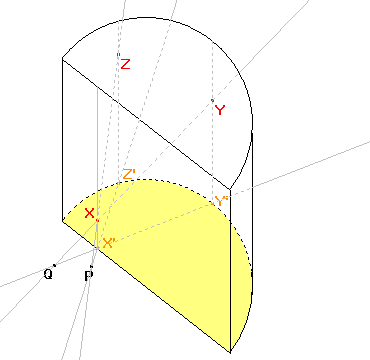 |
Druhý bod získáme pomocí bodů X, Y. Obrazem přímky XY v zadané osové afinitě je přímka X'Y', protože obrazem bodu X je bod X' a bodu Y je bod Y'. Průsečíkem přímky XY a přímky X'Y' je samodružný bod Q, který bude ležet na ose afinity. |
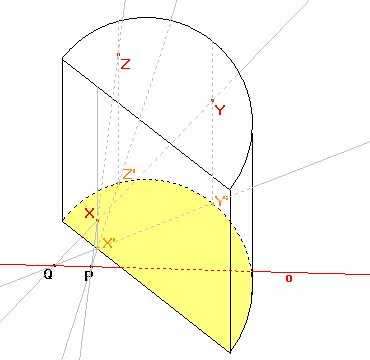 |
Pomocí bodů P, Q již můžeme sestrojit osu afinity o. |
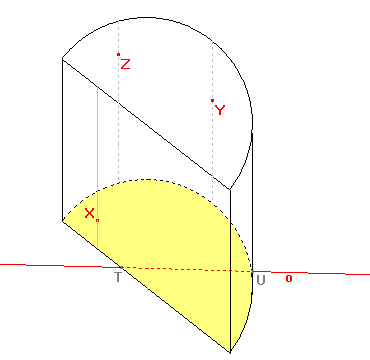 |
K sestrojení elipsy, jejíž část je průsečnicí pláště daného tělesa a roviny řezu, nám stačí pět bodů. Body Y, Z jsou body průsečnice, protože leží na povrchu válce. Osa afinity leží v rovině dolní podstavy tělesa a protíná hranici podstavy, proto průsečíky T, U osy afinity s hraniční kružnicí dolní podstavy jsou body řezu a současně TU je hranicí řezu. |
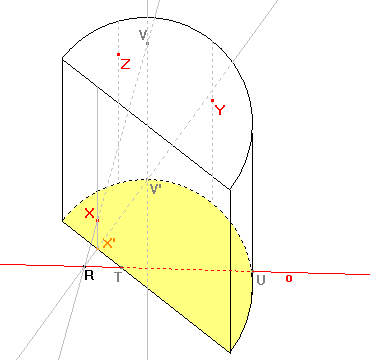 |
Další bod získáme pomocí bodů X, X' a V', kde bod X' je obraz bodu X a bod V' zvolíme libovolně na hranici dolní podstavy tělesa. Bodem V' vedeme rovnoběžku se směrem afinity. Bod R je průsečík přímky X'V' s osou o. Vzorem přímky X'V' je přímka XR a tedy průsečík přímky XR s rovnoběžkou se směrem s v bodě V' je bod elipsy V. |
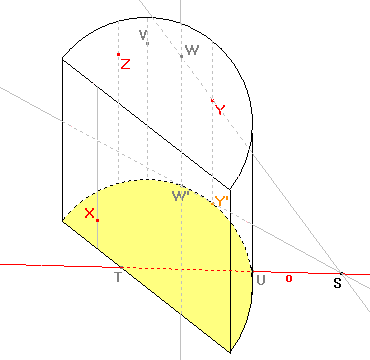 |
Pátý bod získáme pomocí bodů Y, Y' a W', kde bod Y' je obraz bodu Y a bod W' zvolíme libovolně na hranici dolní podstavy tělesa. Bodem W' vedeme rovnoběžku se směrem afinity. Bod S je průsečík přímky Y'W' s osou o. Vzorem přímky Y'W' je přímka YS a tedy průsečík přímky YS s rovnoběžkou se směrem s v bodě W' je bod elipsy W. |
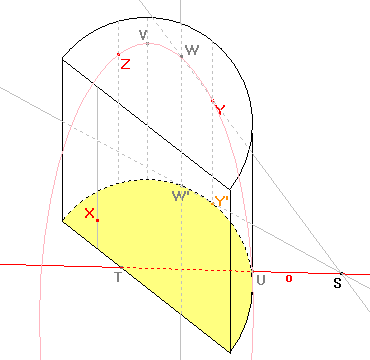 |
Pomocí bodů Y, Z, U, V, W již můžeme sestrojit elipsu, jejíž část bude průsečnicí pláště daného tělesa a roviny řezu. |
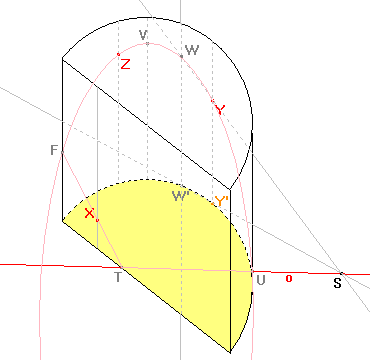 |
Ještě potřebujeme najít hranici řezu v "přední" stěně. Touto hranicí je úsečka FT, protože body F, T leží ve stejné rovině a bod F je průsečík elipsy a "přední" stěny. |
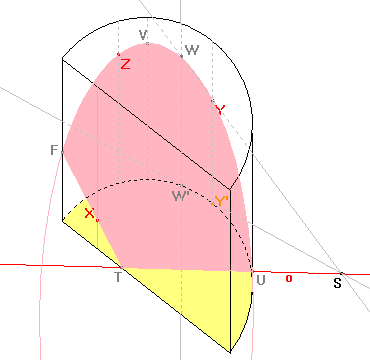 |
Nyní známe vše potřebné k sestrojení řezu daného tělesa. |