Quételetova - Dandelinova věta
Řez rotačního kužele rovinou
V této kapitole si ukážeme, že řezem rotační kuželové plochy rovinou může být elipsa, parabola či hyperbola nebo také další (ovšem singulární) kuželosečky.
Nás budou především zajímat řezy rovinami, které neprochází vrcholem rotačního kužele. (Roviny procházející vrcholem se nazývají vrcholové.) Konkrétně o těchto řezech hovoří tzv. Quételetova - Dandelinova věta.(citace z: Pomykalová [11] str. 272)
Věta K5.1 (Quételet, Dandelin): Řezy rotační kuželové plochy rovinami, které nejsou vrcholové, jsou kuželosečky s ohnisky v dotykových bodech kulových ploch vepsaných kuželové ploše a dotýkajících se roviny řezu.
Quételetova - Dandelinova věta říká dvě důležité věci. První, že řezem rotační kuželové plochy jsou "opravdu" kuželosečky a druhou, kde leží ohniska těchto kuželoseček.
Nejprve budeme klasifikovat jednotlivé řezy pomocí věty K5.2, která je jakýmsi dovětkem věty K5.1. Potom si vše dokážeme. (čerpáno z [W3] str. 21)
Věta K5.2: Jestliže rovina protíná všechny povrchové přímky rotační kuželové plochy, je řezem elipsa. Je-li rovina řezu rovnoběžná právě s jednou površkou plochy, pak je řezem parabola. Pokud je rovina řezu rovnoběžná se dvěma površkami plochy, je řezem hyperbola a ony povrchové přímky udávají směry asymptot.
Označme rovinu řezu \rho. Dále označme \alpha odchylku roviny řezu \rho od roviny libovolné povrchové kružnice kuželové plochy a \beta označíme odchylku povrchových přímek plochy od roviny povrchové kružnice.
Má-li se jednat o tzv. eliptický řez kuželové plochy, rovina má podle věty K5.2 protnout všechny její površky. To nastane právě tehdy, když \alpha < \beta , viz obrázek K5.1 a), kde je nárys dané situace. Je-li navíc rovina \rho kolmá k ose této plochy (\alpha = 0), pak je řezem kružnice jakožto speciální případ elipsy.
V případě tzv. parabolického řezu musí, po obdobné úvaze, nastat rovnost odchylek: \alpha = \beta. Situace je znázorněna na obrázku K5.1 b).
Poslední možností je tzv. hyperbolický řez a to, když \alpha > \beta (obrázek K5.1 c)).
Pozn. k obrázku K5.1: Průmětnu volíme tak, že obsahuje osy o daných kuželových ploch. Rovina řezu \rho je k průmětně kolmá, zobrazuje se jako přímka. Průměty řezů jsou částmi této přímky. Libovolná povrchová kružnice kuželové plochy se zobrazuje jako úsečka kolmá k její ose. Tento způsob zobrazení bude použit i v ostatních obrázcích této kapitoly, ovšem objekty budou pro jednoduchost popisovány bez 2 v dolním indexu (což značí, že se jedná o nárys).
Obrázek K5.1: Klasifikace rovinných řezů rotační kuželové plochy: a) eliptický řez, b) parabolický řez, c) hyperbolický řez
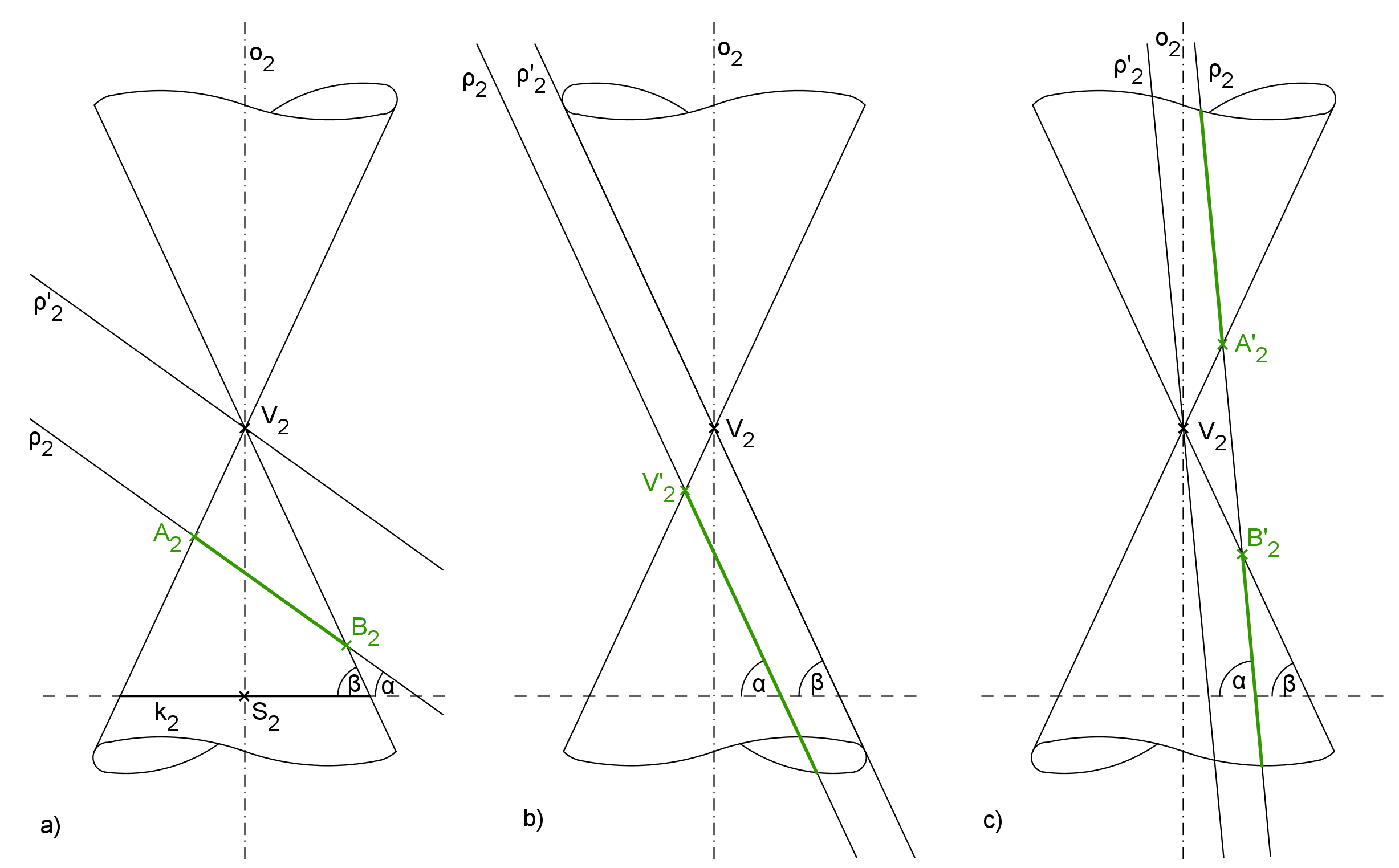
Na obrázku K5.1 jsou u každého řezu navíc znázorněny řezy vrcholovými rovinami \rho ', které jsou rovnoběžné s rovinami \rho. Výsledkem jsou také kuželosečky ovšem singulární. Jsou to postupně:
a) bod - vrchol kuželové plochy;
b) přímka procházející vrcholem kuželové plochy - jedna její površka;
c) dvě různoběžné přímky se společným bodem - vrcholem kuželové plochy.
Zaměříme se na každý z výše uvedených řezů zvlášť a dokážeme, že pro ně platí Věta K5.1 (Quételet, Dandelin).
Eliptický řez rotační kuželové plochy
Jestliže rovina \rho není rovnoběžná se žádnou povrchovou přímkou rotační kuželové plochy, pak kuželosečkou řezu je elipsa (resp. kružnice, je-li rovina \rho kolmá k ose plochy). Podle Quételetovy - Dandelinovy věty (Věty K5.1) jsou její ohniska dotykové body vepsaných sfér do kuželové plochy, které se taktéž dotýkají roviny \rho.
V Apletu K5.1 je nárys části kuželové plochy. Je zde zobrazena rovina \rho, jejíž polohu můžete měnit pomocí bodů A', \, B'. Změnou polohy roviny \rho se budou měnit vepsané sféry a tedy i dotykové body - ohniska elipsy řezu. Vpravo je potom skutečná velikost řezu - elipsy.
Aplet K5.1: Eliptický řez rotační kuželové plochy; skutečný obraz řezu.
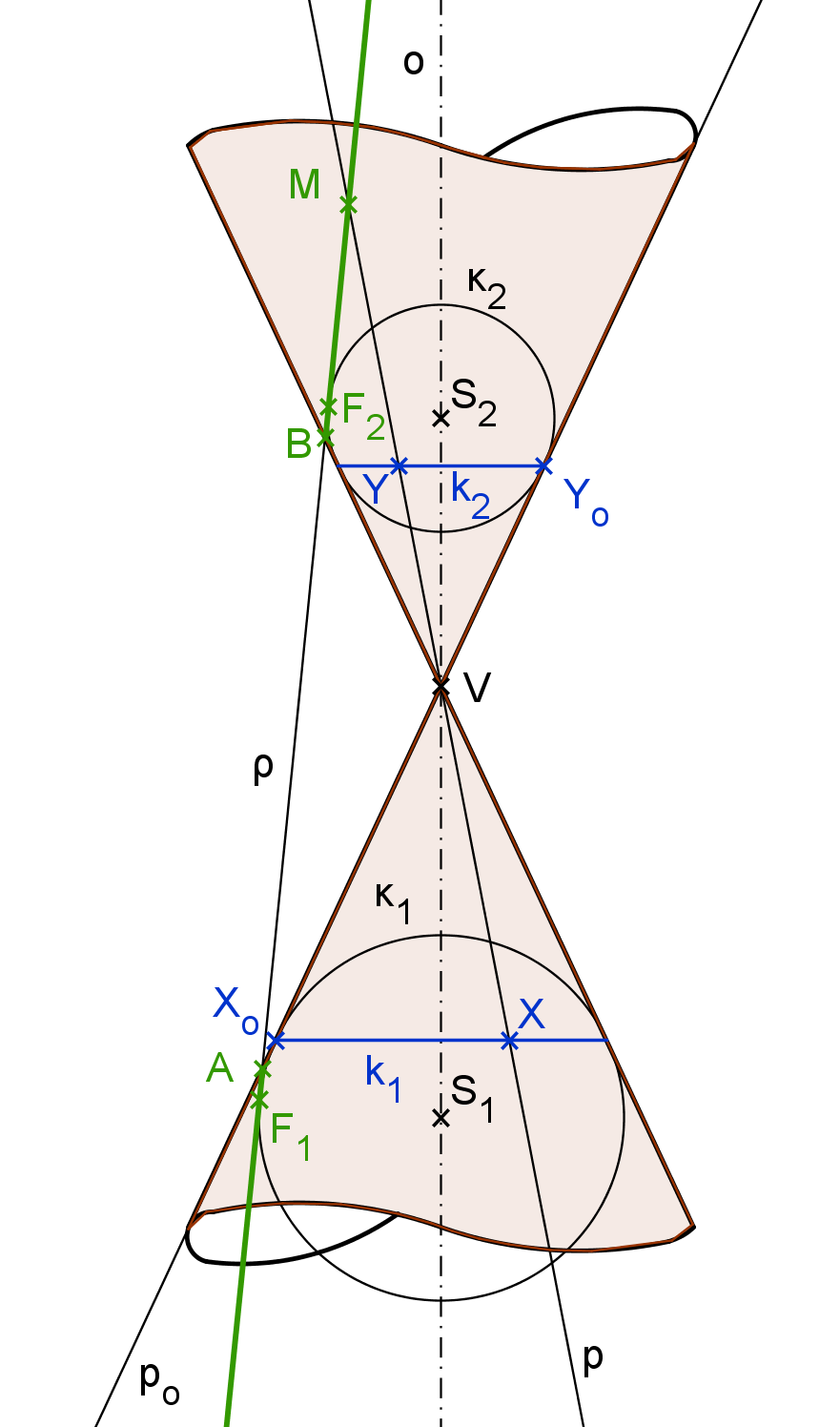
Důkaz Věty K5.1 (Quételet, Dandelin pro elipsu): (obrázek K5.2)
Nechť je dána kuželová plocha K a rovina \rho je rovinou řezu, jež protíná všechny površky
K. Chceme-li dokázat, že průniková křivka je elipsa, musíme dokázat, že její body mají konstantní součet vzdáleností od dvou pevných bodů – ohnisek.
Budeme následovat větu a do kuželové plochy vepíšeme dvě sféry \kappa_1, \, \kappa_2 (dotýkající se plochy K podél kružnic k_1, \, k_2) tak, aby rovina \rho byla jejich společná tečná rovina, body dotyku
nazveme F_1, \, F_2.
Zvolme nyní libovolně bod M = K \cap \rho (chceme dokázat, že leží na elipse). Nechť p je površka jím procházející, přičemž X = p \cap k_1, Y = p \cap k_2.
Platí: |MF_1| = |MX|, protože MF_1 i MX jsou tečny sféry \kappa_1, body F_1 a X jí náleží, tudíž jsou stejně vzdálené od bodu M. Obdobně platí: |MF_2| = |MY|. Odtud |MF_1| + |MF_2| = |MX| + |MY| = |XY|.
Pokud navíc površku p otočíme do polohy p_o (viz. obrázek K5.2), uvidíme ji nezkreslenou. Tedy v tomto otočení můžeme určit skutečnou velikost úsečky XY, |X_oY_o|. Tímto jsme dokázali, že libovolný bod řezu má od bodů F_1, \, F_2 konstantní vzdálenost |X_oY_o|.
Zbývá dokázat, že |X_oY_o| = |AB| = 2a (body A, \, B viz obrázek K5.2).
Platí: |Y_oB| = |BF_2| a |X_oB| = |BF_1|, jelikož Y_oB, \,BF_2 jsou tečny sféry \kappa_2 z bodu B. Obdobně X_oB a BF_1 jsou tečny sféry \kappa_1.
Dále platí:
|AF_1| + |AF_2| = |BF_1| + |BF_2|
2|AF_1| + |F_1F_2| = 2|BF_2| + |F_1F_2| => |AF_1| = |BF_2|
Odtud plyne následující: |X_oY_o| = |X_oB| + |BY_o| = |BF_1| + |F_2B| = |BF_1| + |F_1A| = |AB| := 2a
To znamená, že každý bod řezu je bodem elipsy, jejíž ohniska jsou body F_1, \, F_2 a hlavní poloosa je a = \frac {|AB|} {2}.
Snadno zjistíme, že obráceně každý bod elipsy je také bodem řezu a tím je věta dokázána.
Obrázek K5.2: Důkaz eliptického řezu
Parabolický řez rotační kuželové plochy
Jestliže rovina \rho je rovnoběžná právě s jednou povrchovou přímkou rotační kuželové plochy, pak je řezem parabola. Její ohnisko je dotykovým bodem sféry vepsané do kuželové plochy (podle Věty K5.1).
V Apletu K5.2 je nárys části kuželové plochy. Je zde zobrazena rovina \rho, jejíž polohu můžete měnit pomocí bodu V'. Změnou polohy roviny \rho se bude měnit vepsaná sféra a tedy i dotykový bod - ohnisko paraboly řezu. Vpravo je potom skutečná velikost řezu - paraboly.
Aplet K5.2: Parabolický řez rotační kuželové plochy; skutečný obraz řezu.
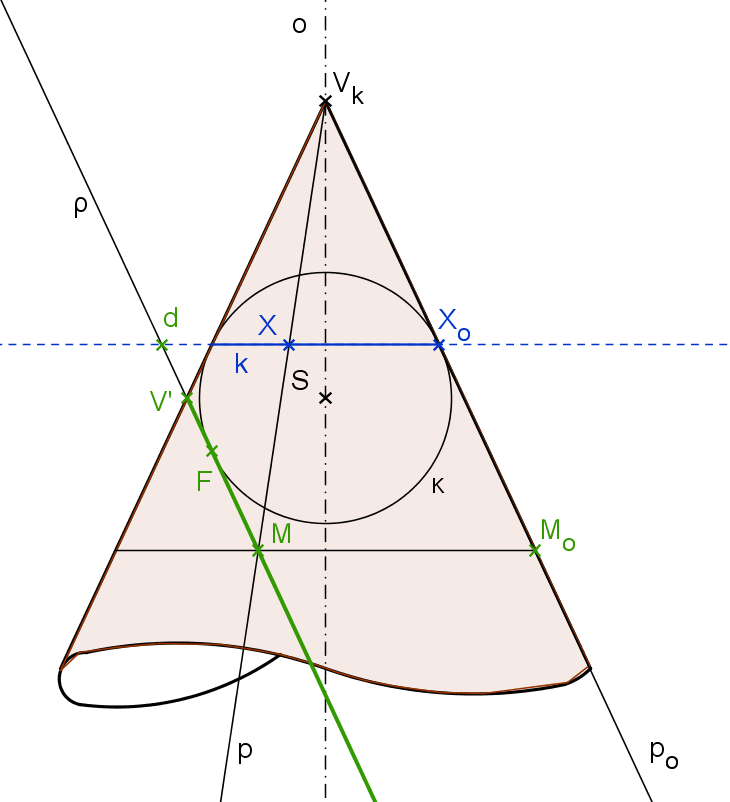
Důkaz Věty K5.1 (Quételet, Dandelin pro parabolu):
(obrázek K5.3; důkaz čerpán z Pomykalová [11] str. 273, 274)
Nechť je dána kuželová plocha K a rovina \rho je rovinou řezu. \rho není vrcholová rovina a je rovnoběžná s jedinou površkou plochy K.
Vepišme do kuželové plochy K kulovou plochu \kappa (dotýkající se plochy K podél kružnice k) tak, aby rovina \rho byla zároveň její tečná rovina. Bod dotyku označme F. Rovina kružnice k protíná rovinu \rho v přímce d (nárysem přímky je bod).
Libovolným bodem M řezu vedeme povrchovou přímku p kuželové plochy K. Přímka p je tečnou kulové plochy \kappa a dotýká se jí v bodě X \in k. Další tečnou kulové plochy procházející bodem M je přímka MF. Délky tečen z bodu ke kulové ploše jsou stejné, proto je |MF| = |MX|. Délku úsečky MX určíme otočením úsečky kolem osy o do nárysny (viz obrázek K5.3). Čtyřúhelník X_oM_oMd je rovnoběžník, proto |M_oX_o| = |Md|. A tedy libovolně zvolený bod M je bodem paraboly s ohniskem F a řídicí přímkou d.
Snadno zjistíme, že obráceně každý bod paraboly je také bodem řezu a tím je věta dokázána.
Obrázek K5.3: Důkaz parabolického řezu
Hyperbolický řez rotační kuželové plochy
Pokud je rovina \rho rovnoběžná se dvěma povrchovými přímkami rotační kuželové plochy, je řezem hyperbola. Její ohniska jsou dotykové body sfér vepsaných do kuželové plochy a dotýkajících se \rho (podle Věty K5.1).
V Apletu K5.3 je nárys části kuželové plochy. Je zde zobrazena rovina \rho, jejíž polohu můžete měnit pomocí bodů A', \, B'. Změnou polohy roviny \rho se budou měnit vepsané sféry a tedy i dotykové body - ohniska hyperboly řezu. Vpravo je potom skutečná velikost řezu - hyperboly.
Aplet K5.3: Hyperbolický řez rotační kuželové plochy; skutečný obraz řezu.
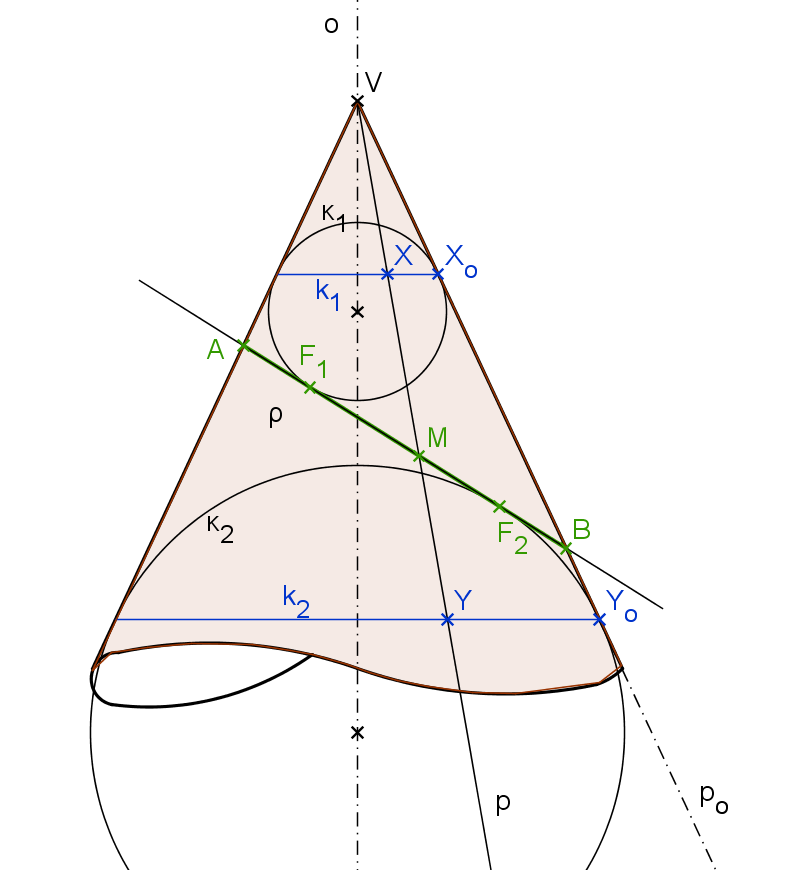
Důkaz Věty K5.1 (Quételet, Dandelin pro hyperbolu):
(obrázek K5.4)
Důkaz pro hyperbolický řez je obdobný důkazu pro eliptický řez.
Nechť je dána kuželová plocha K a rovina \rho je rovinou řezu. \rho není vrcholová rovina a je rovnoběžná se dvěma površkami plochy K.
Vepišme do kuželové plochy K kulové plochy \kappa_1 \, \kappa_2 (dotýkající se plochy K podél kružnic k_1, \, k_2) tak, aby rovina \rho byla zároveň jejich tečná rovina. Body dotyku označme F_1, \, F_2. Chceme-li dokázat, že průniková křivka je hyperbola, musíme dokázat, že všechny body průniku mají konstantní absolutní hodnotu rozdílu vzdáleností od bodů F_1, \, F_2.
Zvolme nyní libovolně bod M = K \cap \rho (chceme dokázat, že leží na hyperbole). Nechť p je površka jím procházející, přičemž X = p \cap k_1, Y = p \cap k_2.
Platí: |MF_1| = |MX|, protože MF_1 i MX jsou tečny sféry \kappa_1, body F_1 a X jí náleží, tudíž jsou stejně vzdálené od bodu M. Obdobně platí: |MF_2| = |MY|. Odtud ||MF_1| - |MF_2|| = ||MX| - |MY|| = |XY|.
Pokud navíc površku p otočíme do polohy p_o rovnoběžné s nárysnou (viz. obrázek K5.4), uvidíme ji v nezkreslené podobě. Můžeme tedy určit skutečnou velikost úsečky XY, |X_oY_o|. Tímto jsme dokázali, že libovolný bod řezu má od bodů F_1, \, F_2 konstantní absolutní hodnotu rozdílu vzdáleností rovnou |X_oY_o|.
Dokážeme ještě, že |X_oY_o| = |AB| = 2a (body A, \, B viz obrázek K5.4).
Platí: |AY_o| = |AF_2| a |AX_o| = |AF_1|, jelikož AY_o, \,AF_2 jsou tečny sféry \kappa_2 z bodu A. Obdobně AX_o a AF_1 jsou tečny sféry \kappa_1.
Dále platí:
|F_1F_2| - 2|AF_1|= |F_1F_2| - 2|BF_2|=> |AF_1| = |BF_2|
Odtud plyne následující: |X_oY_o| = |AY_o| - |AX_o| = |AF_2| - |AF_1| = |AF_2| - |BF_2| = |AB| := 2a
To znamená, že každý bod řezu je bodem hyperboly, jejíž ohniska jsou body F_1, \, F_2 a hlavní poloosa má délku a = \frac {|AB|} {2}.
A naopak snadno zjistíme, že každý bod hyperboly je též bodem řezu a tím je věta dokázána.
Obrázek K5.4: Důkaz hyperbolického řezu