Definice
Definice elipsy
Definice: Nechť jsou v rovině E_2 dány dva různé body F_1 a F_2 a konstanta a>0, pro kterou platí 2a>|F_1F_2|.
Elipsou k_e budeme rozumět množinu všech bodů v rovině E_2, které mají konstantní součet vzdáleností od bodů F_1 a F_2 roven 2a.
k_e= \{ X \in E_2; \, |F_1X| + |XF_2|=2a, \, kde \; 2a>|F_1F_2|\}.
Pozn.: Kdyby v definici elipsy bylo místo "různých bodů" jen "bodů", pak bychom připustili, že ohniska mohou splynout v jeden dvojnásobný bod. Tím bychom mezi elipsy zařadili i kružnici.
Kdyby nebylo řečeno "2a>|F_1F_2|", neboli, že součet průvodičů (průvodič - viz níže) je větší než vzdálenost |F_1F_2|, pak bychom připustili, že součet může být menší nebo roven |F_1F_2|. V prvním případě by neexistoval žádný bod vyhovující daným podmínkám. V druhém případě bychom dostali úsečku s krajními body F_1 a F_2.
Pokud budete v apletu E1.1 pohybovat bodem X po elipse, můžete se přesvědčit, že součet vzdáleností bodu X od pevně zvolených bodů F_1 a F_2 je opravdu konstantní. Součet těchto vzdáleností je počítán v tabulce vpravo nahoře. Také můžete posunout bod F_1 do bodu F_2 a přesvědčit se o tom, že takto dostanete kružnici.
Aplet E1.1: Definice elipsy - konstantní součet průvodičů
Základní pojmy
Nyní vymezíme několik důležitých pojmů vztahujících se k elipse. V dalším textu budou termíny používány.
Body F_1 a F_2 nazýváme ohniska elipsy (někdy také fokusy z latinského slova focus, což znamená ohnisko). Z definice tedy plyne, že každá elipsa má dvě ohniska, dva různé pevně dané body. Pokud by toto neplatilo a ohniska by mohla splynout v jeden bod, výslednou křivkou by byla nikoliv elipsa, ale kružnice. O tomto se můžete taktéž přesvědčit v apletu výše, pokud posunete jedno ohnisko do druhého. Také je při tom dobře vidět jak závisí tvar elipsy na vzdálenosti obou ohnisek. (O tvaru elipsy najdete v textu více později.)
Vzdálenosti, nebo také spojnice F_1X, F_2 X libovolného bodu X \in k_e a ohnisek se nazývají průvodiče bodu X. V apletu jsou značeny jako p_1 a p_2. Ovšem někdy se značí také r_1, r_2 podle latinského názvu radius = průvodič.
Přímku F_1 F_2 budeme značit o_1. Jedná se o hlavní osu elipsy. Přímka kolmá na hlavní osu o_1 procházející bodem S, který je středem úsečky F_1 F_2, se nazývá vedlejší osa elipsy a značí se o_2. Bod S je zároveň středem elipsy.
Body A, B, které jsou průsečíky hlavní osy o_1 a elipsy, se nazývají hlavní vrcholy. Obdobně průsečíky vedlejší osy o_2 a elipsy, budeme značit C, D a nazývat vedlejší vrcholy elipsy.
Podle definice platí, že součet délek průvodičů libovolného bodu elipsy je roven konstantě 2a>0. Platí-li tento vztah pro každý bod ležící na elipse, musí tedy platit i pro hlavní vrcholy A, B.Tudíž platí následující rovnosti:
|AF_1| + |AF_2| = |BF_1| + |BF_2| = 2a
|AF_2| = |AF_1| + |F_1F_2| = |F_2B| + |F_1F_2| = |BF_1|
2a = |AF_1| + |AF_2| = |AF_1| + |F_1F_2| + |F_2B| = |AB|
Tedy:
2a = |AB|
a = |AS| = |BS|.
Z předchozího vyplývá, že konstanta a představuje délku úsečky AS či SB. Konstantu a budeme nazývat délka hlavní poloosy. Zavedeme další konstantu b a budeme jí nazývat délka vedlejší poloosy. Stejně tak jako platí a = |AS| = |SB|, platí také b = |CS| = |SD|.
Další důležitou konstantou je tzv. excentricita, neboli lineární výstřednost. Značí se e a určuje vzdálenost ohniska od středu elipsy (název pochází z latiny, ex = mimo, centrum = střed). Vyjadřuje tedy délku úsečky F_1S či F_2S.
Všechny výše uvedené konstanty, body a přímky jsou vyznačené na obrázku E1.1.
Obrázek E1.1: Elipsa
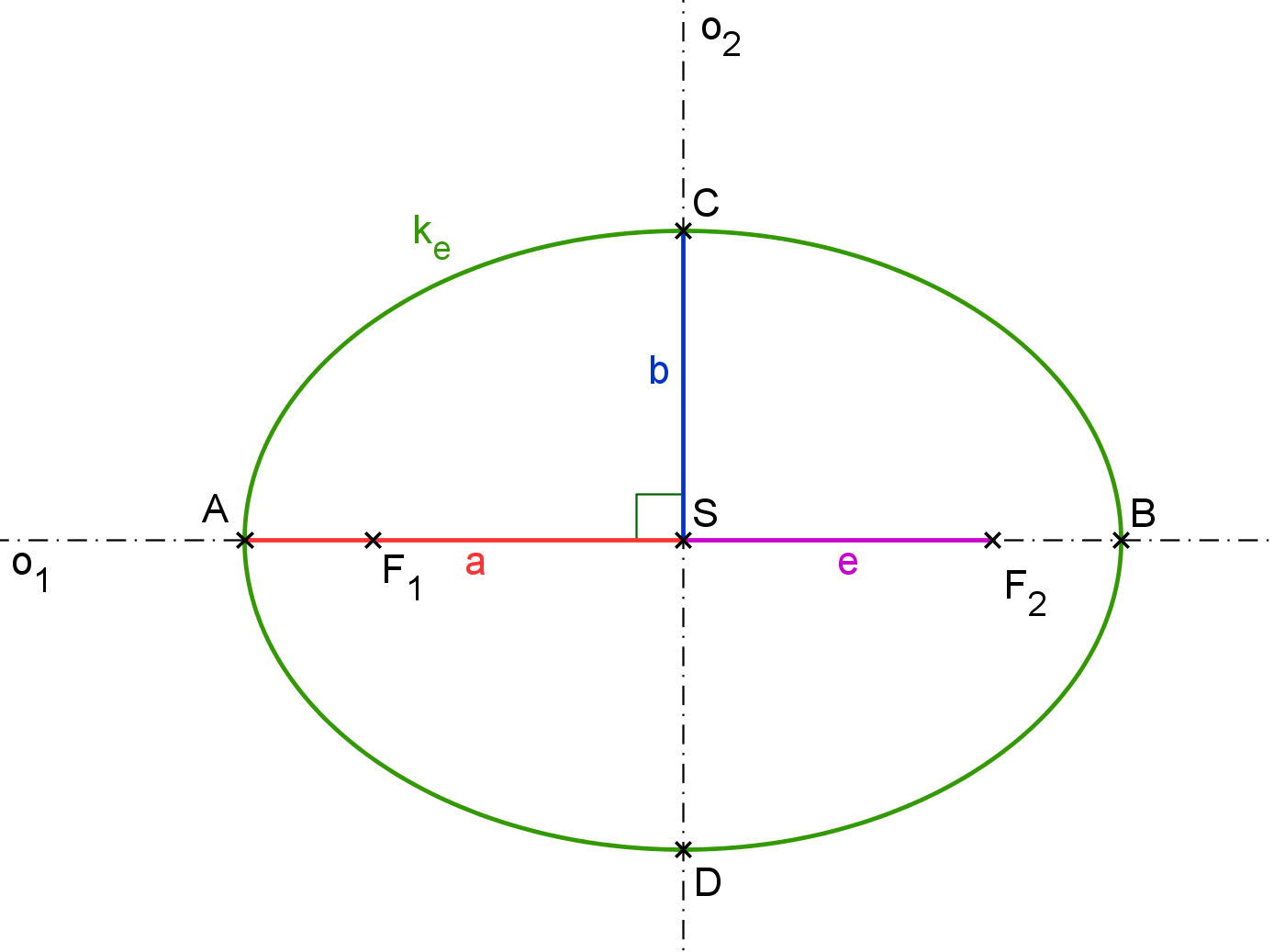
Pro větší přehlednost a ucelenost termínů je zde tabulka, která shrnuje všechny pojmy:
| označení | název | definice |
|---|---|---|
| k_e | elipsa | |
| F_1, F_2 | ohniska (fokusy) | |
| A, B | hlavní vrcholy | průsečíky o_1 a k_e |
| C, D | vedlejší vrcholy | průsečíky o_2 a k_e |
| S | střed elipsy | střed úsečky F_1F_2 |
| o_1 | hlavní osa | přímka AB |
| o_2 | vedlejší osa | přímka CD |
| a | délka hlavní poloosy | |AS| či |SB| |
| b | délka vedlejší poloosy | |CS| či |SD| |
| e | excentricita (výstřednost) | |F_1S| či |SF_2| |