n-tá mocnina komplexního čísla
V kapitole Násobení komplexních čísel v goniometrickém tvaru jsme vzorec pro násobení dvou komplexních čísel
zobecnili pro 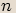 činitelů, kde
činitelů, kde 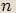 je přirozené číslo, čímž jsme dostali
je přirozené číslo, čímž jsme dostali  .
.
Pokud platí, že  , pak vynásobením těchto
, pak vynásobením těchto 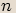 čísel dostaneme
čísel dostaneme 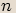 -tou mocninu čísla
-tou mocninu čísla  .
Odtud plyne vztah pro
.
Odtud plyne vztah pro 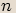 -tou mocninu komplexního čísla
-tou mocninu komplexního čísla  .
.
Definice
Mocnina komplexního čísla
Máme-li komplexní číslo  zapsané ve tvaru
zapsané ve tvaru  , pak
n-tou mocninou tohoto komplexního čísla, kde
, pak
n-tou mocninou tohoto komplexního čísla, kde 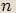 je přirozené číslo, nazveme komplexní číslo
je přirozené číslo, nazveme komplexní číslo  .
Tuto mocninu značíme
.
Tuto mocninu značíme  .
.
Je-li  , pak
, pak  .
.
Moivreova věta
Pro každé přirozené číslo 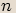 a libovoné reálné číslo
a libovoné reálné číslo  platí
platí  .
.
Poznámka
Vzorec  platí i pro
platí i pro  .
.
Moivreovu větu můžeme použít k vyjádření funkcí  ,
,  ,
pomocí funkcí
,
pomocí funkcí  ,
,  , kde
, kde  je přirozené číslo.
je přirozené číslo.
Řešený příklad
Vyjádřete  a
a  pomocí funkcí
pomocí funkcí  a
a  .
.
Využijeme Moivreovu větu: 
Využijeme binomickou větu: 

Užitím pravidla, že dvě komplexní čísla se rovnají, pokud se rovnají jejich reálné a
imaginární složky, dostáváme ,
,
 .
.
Použijeme-li vztah  , můžeme je dále upravit na tvar
, můžeme je dále upravit na tvar ,
,
 .
.
Příklady
























n-tá odmocnina z komplexního čísla
Definice
n-tou odmocninou , kde 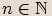 , z komplexního čísla
, z komplexního čísla  nazveme každé
komplexní číslo
nazveme každé
komplexní číslo  , pro které platí
, pro které platí 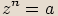 .
.
 K určení
K určení 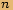 -té odmocniny z čísla
-té odmocniny z čísla  stačí řešit rovnici
stačí řešit rovnici  .
.
Poznámka
Každé řešení rovnice 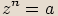 je
je 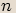 -tou odmocninou z čísla
-tou odmocninou z čísla  .
.
Je-li  , pak pro libovolné
, pak pro libovolné 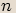 má rovnice
má rovnice  právě jedno řešení
právě jedno řešení  .
.
Je-li  , pak také
, pak také  . Vyjádříme-li obě čísla v goniometrickém tvaru
. Vyjádříme-li obě čísla v goniometrickém tvaru  ,
,  , pak rovnice
, pak rovnice
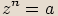 má tvar
má tvar  .
.
Dvě komplexní čísla se rovnají, pokud jsou si rovny jejich absolutní hodnoty
a zároveň pokud se jejich argumenty rovnají nebo liší o celočíselný násobek 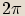 .
Proto z odvozené rovnosti plyne, že
.
Proto z odvozené rovnosti plyne, že a
a
 neboli
neboli a
a
 .
.
Podle toho všechna řešení rovnice 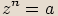 (tedy
(tedy 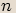 -té odmocniny z čísla
-té odmocniny z čísla  ) můžeme zapsat ve tvaru
) můžeme zapsat ve tvaru
 ,
kde
,
kde  . Pro další
. Pro další 
už nedostaneme nová řešení, protože argumenty se budou lišit o celočíselný
násobek 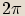 .
.
Vidíme tedy, že všechny 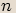 -té odmocniny z
-té odmocniny z  mají stejnou absolutní hodnotu
mají stejnou absolutní hodnotu  a jejich argumenty
a jejich argumenty
se liší o násobek  .
.
To znamená, že obrazy komplexních čísel, která jsou 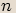 -tými odmocninami
z čísla
-tými odmocninami
z čísla  pro
pro  , jsou vrcholy pravidelného
, jsou vrcholy pravidelného 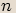 -úhelníka vepsaného do kružnice se středem v počátku
a poloměrem
-úhelníka vepsaného do kružnice se středem v počátku
a poloměrem  . Pro
. Pro  jsou komplexními odmocninami dvě opačná komplexní čísla.
jsou komplexními odmocninami dvě opačná komplexní čísla.
Všechny předcházející poznatky lze shrnout do následující věty.
Věta
Odmocniny komplexního čísla
Je-li  nenulové komplexní číslo a
nenulové komplexní číslo a 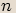 je celé kladné číslo, pak existuje právě
je celé kladné číslo, pak existuje právě 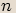 komplexních
čísel, která jsou
komplexních
čísel, která jsou 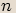 -tou odmocninou z
-tou odmocninou z  , tj. takových čísel
, tj. takových čísel  , že
, že 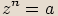 . Jsou to čísla
. Jsou to čísla
 ,
,
kde  .
.
 Vyplývá z poznámky před větou.
Vyplývá z poznámky před větou.
Příklady



 Číslo
Číslo  zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.


 , kde
, kde 













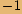 zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.

 , kde
, kde 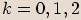











 zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.

 , kde
, kde 




