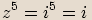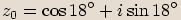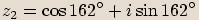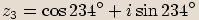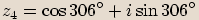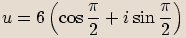 ,
, 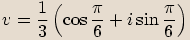 . Výsledky vyjádřete v algebraickém tvaru.
. Výsledky vyjádřete v algebraickém tvaru.

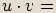
 Při počítání součinu čísel v goniometrickém tvaru absolutní hodnoty čísel násobíme a
argumenty sčítáme.
Při počítání součinu čísel v goniometrickém tvaru absolutní hodnoty čísel násobíme a
argumenty sčítáme.
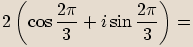

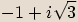
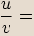
 Při počítání podílu absolutní hodnoty dělíme a argumenty odčítáme.
Při počítání podílu absolutní hodnoty dělíme a argumenty odčítáme.
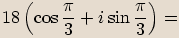

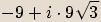

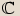 :
:
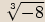

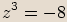

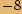 zapíšeme v goniometrickém tvaru a určíme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a určíme všechna řešení rovnice.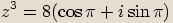

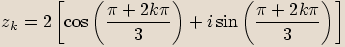 , kde
, kde 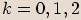

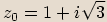



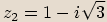

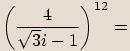

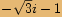 .
.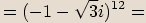

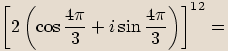

a argument čísla vynásobíme mocnitelem.
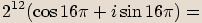

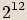

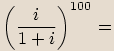

 .
.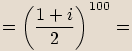

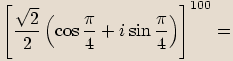

a argument čísla vynásobíme mocnitelem.
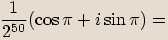

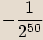

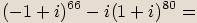

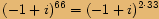
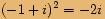
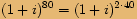
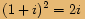
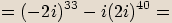

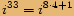
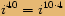
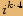 , kde
, kde 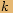 je celé číslo, je rovno jedné.
je celé číslo, je rovno jedné.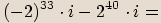

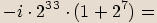

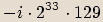

 rovnice:
rovnice:
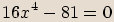 (řešte pomocí vzorce pro výpočet
(řešte pomocí vzorce pro výpočet 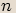 -té
odmocniny)
-té
odmocniny)

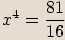
 Číslo
Číslo 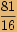 zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
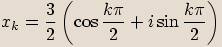 , kde
, kde 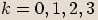

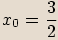

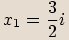

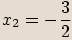

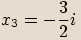

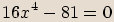 (řešte pomocí rozkladu na součin mnohočlenů)
(řešte pomocí rozkladu na součin mnohočlenů)

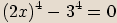
 Levou stranu rovnice rozložíme na součin mnohočlenů.
Levou stranu rovnice rozložíme na součin mnohočlenů.
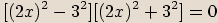
 První dvojčlen rozložíme dále na součin mnohočlenů.
První dvojčlen rozložíme dále na součin mnohočlenů.
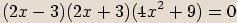
 První dvojčlen položíme roven nule.
První dvojčlen položíme roven nule.
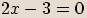

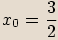
 Druhý dvojčlen položíme roven nule.
Druhý dvojčlen položíme roven nule.
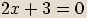

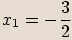
 Třetí dvojčlen položíme roven nule.
Třetí dvojčlen položíme roven nule.
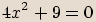
 Vyřešíme kvadratickou rovnici.
Vyřešíme kvadratickou rovnici.
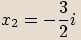

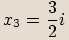

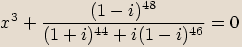

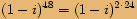
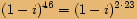
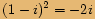
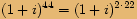
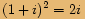
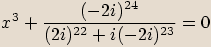

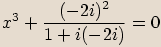

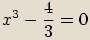

 zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.

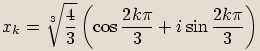 , kde
, kde 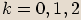

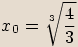

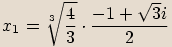

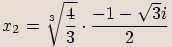

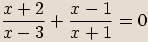

 .
.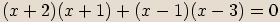

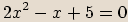

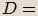

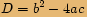
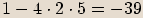
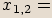

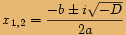
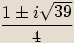

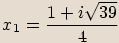

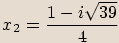

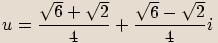 . Vypočítejte a zapište v algebraickém tvaru
. Vypočítejte a zapište v algebraickém tvaru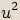 ,
,
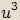 ,
,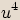 .
.
 Číslo
Číslo 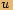 zapíšeme v goniometrickém tvaru, tedy spočítáme jeho absolutní hodnotu a argument.
zapíšeme v goniometrickém tvaru, tedy spočítáme jeho absolutní hodnotu a argument.
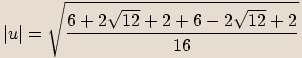

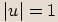

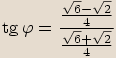

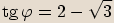

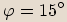

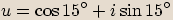
 Při umocňování absolutní hodnotu čísla umocňujeme a argument násobíme mocnitelem.
Při umocňování absolutní hodnotu čísla umocňujeme a argument násobíme mocnitelem.


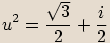

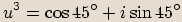

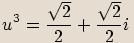



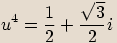

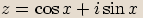 , vypočítejte
, vypočítejte 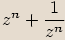 ,
, 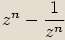 . Výsledky uveďte v goniometrickém tvaru.
. Výsledky uveďte v goniometrickém tvaru.

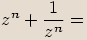
 Při umocňování absolutní hodnotu čísla umocňujeme a argument násobíme mocnitelem.
Při umocňování absolutní hodnotu čísla umocňujeme a argument násobíme mocnitelem.
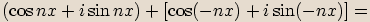



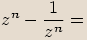
 Při umocňování absolutní hodnotu čísla umocňujeme a argument násobíme mocnitelem.
Při umocňování absolutní hodnotu čísla umocňujeme a argument násobíme mocnitelem.
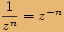
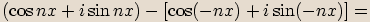

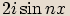

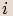 . Určete komplexní čísla v goniometrickém tvaru, jejichž obrazy jsou zbývající vrcholy
pětiúhelníka.
. Určete komplexní čísla v goniometrickém tvaru, jejichž obrazy jsou zbývající vrcholy
pětiúhelníka.  Jeden vrchol je číslo
Jeden vrchol je číslo  a vrcholů má být celkem pět, takže budeme řešit rovnici
a vrcholů má být celkem pět, takže budeme řešit rovnici
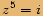 .
.