Komplexní čísla jako body Gaussovy roviny

Komplexní čísla znázorňujeme jako body roviny, ve které je zavedena kartézská soustava souřadnic. Tato rovina se nazývá rovina komplexních čísel nebo také Gaussova rovina.

Každé komplexní číslo 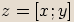je v ní znázorněno bodem 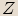o souřadnicích 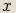a 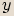. Přiřazení mezi komplexními čísly a body Gaussovy roviny je vzájemně jednoznačné.

Každému komplexnímu číslu je přiřazen právě
jeden bod Gaussovy roviny jako jeho obraz
a naopak každému bodu Gaussovy roviny je
přiřazeno právě jedno komplexní číslo
jako jeho vzor.

Osa 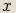se v Gaussově rovině nazývá osa reálných čísel, neboli reálná osa. Osa 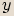se v této rovině nazývá osa ryze imaginárních čísel, neboli imaginární osa.

Obrazy reálných čísel leží v Gaussově rovině na reálné ose, obrazy imaginárních čísel jsou ty body Gaussovy roviny, které neleží na reálné ose. Obrazy ryze imaginárních čísel leží na imaginární ose.

>>nahoru<<

Komplexní čísla jako polohové vektory

Každému bodu 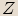Gaussovy roviny lze přiřadit polohový vektor 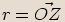, kde je počátek kartézské soustavy souřadnic. Tedy i každému komplexnímu číslu 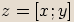lze přiřadit polohový vektor, jehož počáteční bod je počátek soustavy souřadnic a koncový bod je bod o souřadnicích .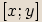

Protože každému vektoru o souřadnicích 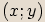lze přiřadit právě jedno komplexní číslo, a to komplexní číslo 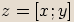, je přiřazení mezi komplexními čísly a polohovými vektory vzájemně jednoznačné.

Geometrické znázornění komplexních čísel pomocí polohových vektorů je výhodné při znázorňování operací s komplexními čísly.

>>nahoru<<

Geometrický význam absolutní hodnoty

Absolutní hodnota komplexního čísla je rovna vzdálenosti bodu, který je obrazem tohoto čísla v Gaussově rovině, od počátku soustavy souřadnic. Značíme ji .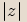

Všechna komplexní čísla , která mají stejnou absolutní hodnotu, vyplní v Gaussově rovině kružnici se středem v počátku a s poloměrem rovným číslu .

Pro komplexní jednotky má tato kružnice poloměr roven jedné.

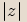Absolutní hodnota rozdílu dvou komplexních čísel určuje vzdálenost bodů, které jsou obrazy těchto komplexních čísel v Gaussově rovině.

>>nahoru<<

Znázornění komplexně sdružených čísel

Máme-li dvě čísla navzájem komplexně sdružená, pak body, které jsou jejich obrazy v Gaussově rovině, jsou osově souměrné podle osy 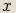, protože tato dvě čísla se liší znaménkem u druhé složky.

>>nahoru<<

Znázornění opačných čísel

Znázorňujeme-li v Gaussově rovině dvě čísla navzájem opačná, pak body, které jsou jejich obrazy, jsou souměrné podle počátku, protože se tato dvě čísla liší znaménky u obou složek.

>>nahoru<<

Znázornění součtu a rozdílu komplexních čísel

Komplexní čísla zobrazujeme jako polohové vektory.

Při sčítání komplexních čísel sčítáme příslušné vektory.

Při odčítání komplexních čísel odčítáme příslušné vektory.

Poznámka

Násobení a dělení je výhodné znázorňovat, jsou-li čísla v goniometrickém tvaru, jak uvidíme po zavedení komplexních čísel v goniometrickém tvaru.

Součin komplexních čísel v goniometrickém tvaru
Podíl komplexních čísel v goniometrickém tvaru

>>další stránka<<>>nahoru<<