Obor komplexních čísel vznikl rozšířením oboru reálných čísel.

V oboru reálných čísel je definováno sčítání, násobení, odčítání a dělení libovolných čísel (kromě dělení nulou). Pro reálné číslo je definována také 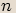-tá mocnina, kde 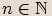. Avšak 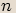-tá odmocnina,
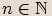, je definována pouze z nezáporného čísla. Z toho plyne, že v oboru reálných čísel jsou řešitelné pouze kvadratické rovnice s nezáporným diskriminantem. A právě proto, aby například i kvadratická rovnice typu 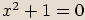měla řešení, byl obor reálných čísel 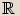rozšířen na obor komplexních čísel, který značíme .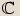

Komplexní čísla jsou tedy abstraktním oborem, ve kterém je definována odmocnina z každého čísla.

S applety na těchto stránkách můžeme pracovat pouze na počítači, na kterém máme nainstalovaný programovací jazyk Java, nebo alespoň prostředí Java Runtime Environment (JRE). Obojí je možné zdarma stáhnout z Internetu na adrese http://java.com.

Do textových polí appletu zapíšeme komplexní číslo, které chceme zobrazit, a stiskneme tlačítko "OK" (v appletu) nebo klávesu "Enter" (na klávesnici). Hodnoty v těchto polích jsou implicitně nastaveny na , takže po stisknutí tlačítka "OK" bude zobrazeno číslo 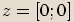. Poté můžeme vykreslený bod (obraz čísla ) uchopit levým tlačítkem myši a libovolně s ním pohybovat. Přitom hodnoty v textových polích budou aktualizovány podle právě zobrazovaného komplexního čísla. Tyto hodnoty jsou v případě uspořádaných dvojic a algebraického tvaru uváděny s přesností na jedno desetinné místo, v případě goniometrického tvaru na dvě desetinná místa. Velikosti úhlů v goniometrickém tvaru jsou hodnoty z intervalu . 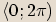Vykreslit lze pouze komplexní číslo, jehož reálná i imaginární část je z intervalu 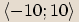. Pokud se v textových polích výsledku objeví písmeno "N", znamená to, že požadovanou operaci nelze provést, protože výraz není definován. Pokud se po zadání operace nic neprovede, znamená to, že čísla na vstupu jsou chybná, například bylo zadáno písmeno místo číslice, a je třeba vstupní hodnoty opravit.

Popisek pod appletem nám říká, co vše bude applet zobrazovat. Applet v použitém příkladu zobrazí zadané číslo a číslo k němu komplexně sdružené. Obraz komplexně sdruženého čísla je závislý na zadaném čísle, proto lze hýbat pouze obrazem zadaného čísla.

Applety pro 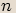-tou mocninu a odmocninu mají navíc další textové pole. Jeho hodnota udává, kolikátá mocnina či odmocnina ze zadaného čísla bude počítána.

Se "smajlíkem" se můžeme setkat u definic a matematických vět.

V případě definice je pod ním ukryto takzvané vysvětlení definice, které nemusí být vždy matematicky úplně přesné, ale může být srozumitelnější pro čtenáře. Toto pomocné vysvětlení se zobrazí po nastavení myši na "smajlíka", který se v tu chvíli změní na .

V případě vět je pod ním ukryt důkaz, který můžeme zobrazit tak, že na "smajlíka" klikneme levým tlačítkem myši. Ten v tu chvíli zmizí a na konci důkazu se zobrazí .

Se "smajlíkem" se setkáme u příkladů.

V případě, že řešení příkladu je obtížné, odkryje se po nastavení myši na "smajlíka" nápověda, jak pokračovat při řešení, a tento "smajlík" se změní na . Po kliknutí levým tlačítkem myši se zobrazí další krok výpočtu s novým "smajlíkem". Pokud je následující krok v řešení jednoduchý a není potřeba nápověda, zůstane "smajlík" po nastavení myši nezměněný a čeká se na kliknutí. Na konci každého příkladu se ukáže .

Poznámka

Webové stránky byly testovány v prohlížečích Mozilla Firefox verze 1.5, Internet Explorer verze 5 a 6, Opera verze 6. Doporučováno je k jejich prohlížení použít prohlížeč Mozilla Firefox, který je možné zdarma stáhnout z Internetu na adrese http://www.mozilla.com/firefox/.