Definice komplexních čísel
Komplexním číslem  nazýváme uspořádanou dvojici reálných čísel
nazýváme uspořádanou dvojici reálných čísel 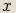 a
a 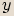 , píšeme
, píšeme 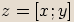 .
Číslu
.
Číslu 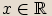 říkáme reálná část komplexního čísla
říkáme reálná část komplexního čísla  ,
číslu
,
číslu 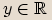 imaginární část komplexního čísla
imaginární část komplexního čísla  .
.
Klasifikace komplexních čísel
Nechť 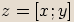 je komplexní číslo.
je komplexní číslo.
Je-li 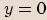 , pak
, pak 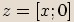 je reálné číslo
a lze použít zápis
je reálné číslo
a lze použít zápis  . Uspořádaná dvojice
. Uspořádaná dvojice  je
pouze jinou formou vyjádření reálného čísla
je
pouze jinou formou vyjádření reálného čísla 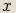 .
.
Je-li 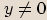 , pak
, pak  nazýváme imaginární číslo.
Je-li zároveň
nazýváme imaginární číslo.
Je-li zároveň  , pak číslu
, pak číslu  říkáme ryze imaginární číslo.
říkáme ryze imaginární číslo.
Rovnost komplexních čísel
Definice
Dvě komplexní čísla ve tvaru uspořádaných dvojic jsou si rovna, právě když jsou si rovny jejich reálné části a jejich imaginární části.
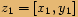
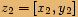
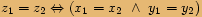 >>nahoru<<
>>nahoru<<
Absolutní hodnota komplexního čísla
Definice
Absolutní hodnotou komplexního čísla  vyjádřeného ve tvaru
vyjádřeného ve tvaru 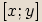 nazveme reálné číslo
nazveme reálné číslo 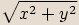 ,
značíme ji
,
značíme ji 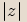 .
.
Komplexní číslo, jehož absolutní hodnota je rovna 1, se nazývá komplexní jednotka.
Příklady komplexních jednotek
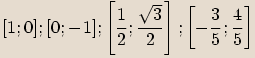
Příklady
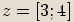

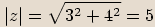

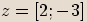

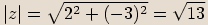

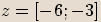

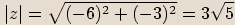

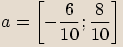
 Číslo
Číslo  je komplexní jednotka, pokud
je komplexní jednotka, pokud 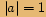 .
.
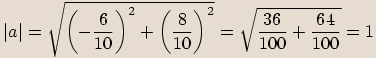

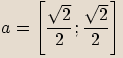
 Číslo
Číslo  je komplexní jednotka, pokud
je komplexní jednotka, pokud 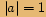 .
.
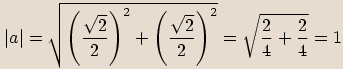

Poznámka
Komplexní čísla nelze uspořádat podle velikosti ani rozlišit na kladná a záporná.
>>nahoru<<Číslo komplexně sdružené
Definice
Číslem komplexně sdruženým ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 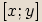 nazýváme komplexní číslo
nazýváme komplexní číslo 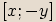 ,
značíme ho
,
značíme ho  .
.
 Číslo
Číslo 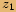 je komplexně sdružené k číslu
je komplexně sdružené k číslu 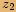 ,
,pokud se tato dvě čísla liší pouze znaménkem
u imaginární části.
Příklady
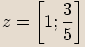

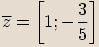

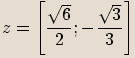

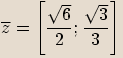

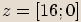

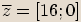

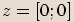

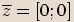

Opačné komplexní číslo
Definice
Opačným číslem ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 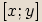 nazýváme číslo
nazýváme číslo 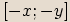 ,
značíme ho
,
značíme ho 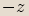 .
.
 Číslo
Číslo 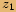 je opačné k číslu
je opačné k číslu 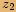 ,
pokud se tato
,
pokud se tato dvě čísla liší znaménky u reálné i imaginární části.
Příklady
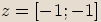

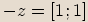

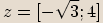

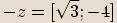

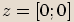

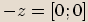

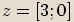

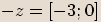

Operace s komplexními čísly ve tvaru uspořádaných dvojic
Definice
Máme-li dvě komplexní čísla 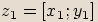 a
a 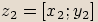 , pak jejich součtem budeme nazývat komplexní číslo
, pak jejich součtem budeme nazývat komplexní číslo 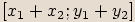 . Tento součet značíme
. Tento součet značíme  .
.
 Sčítání komplexních čísel ve tvaru
Sčítání komplexních čísel ve tvaruuspořádaných dvojic se provádí po
složkách, tzn. sečteme nejprve první
složky a potom druhé složky čísel.
Příklady
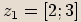 ,
, 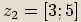

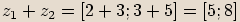

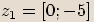 ,
, 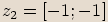

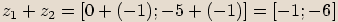

Definice
Máme-li dvě komplexní čísla 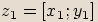 a
a 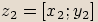 , pak jejich rozdílem budeme nazývat komplexní číslo
, pak jejich rozdílem budeme nazývat komplexní číslo 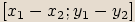 . Tento rozdíl značíme
. Tento rozdíl značíme  .
.
 Odčítání komplexních čísel ve tvaru
Odčítání komplexních čísel ve tvaruusp. dvojic provedeme po složkách,
tzn. nejprve odečteme první složky
a potom druhé složky čísel.
Příklady
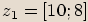 ,
, 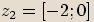

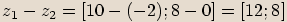

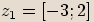 ,
, 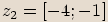

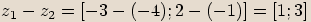

Definice
Máme-li dvě komplexní čísla 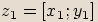 a
a 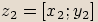 , pak jejich součinem budeme nazývat komplexní číslo
, pak jejich součinem budeme nazývat komplexní číslo 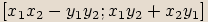 . Tento součin značíme
. Tento součin značíme  .
.
Příklady
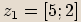 ,
, 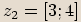

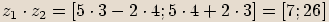

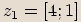 ,
, 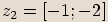

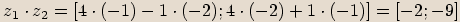

Poznámka
V oboru komplexních čísel (stejně jako v oboru reálných čísel) má sčítání a násobení následující vlastnosti:
- Sčítání a násobení je komutativní.
- Sčítání a násobení je asociativní.
- Násobení je distributivní vzhledem ke sčítání.
- Ke každému číslu existuje jediné opačné číslo.
- Ke každému nenulovému číslu existuje jediné číslo takové, že jejich součin je roven jedné.
- Je-li součin dvou reálných čísel roven nule, je rovno nule aspoň jedno z nich.
Poznámka
Provádět operace s komplexními čísly je výhodnější, jsou-li tato čísla zapsána v algebraickém nebo goniometrickém tvaru. Proto se na tomto místě operacemi nebudeme více zabývat ani je procvičovat. Vrátíme se k nim později, kdy budeme také definovat podíl komplexních čísel.
Sčítání a násobení komplexních čísel v algebraickém tvaruNásobení komplexních čísel v goniometrickém tvaru >>další stránka<<>>nahoru<<