Sčítání a násobení komplexních čísel v algebraickém tvaru
Komplexní čísla v algebraickém tvaru se sčítají a násobí obdobně jako dvojčleny.
Definice
Součet dvou komplexních čísel
Máme-li dvě komplexní čísla 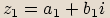 a
a 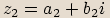 , pak jejich
součtem budeme nazývat komplexní číslo
, pak jejich
součtem budeme nazývat komplexní číslo 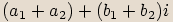 .
Tento součet označujeme
.
Tento součet označujeme  .
.

součtu reálných částí a imaginární část součtu imaginárních
částí všech sčítanců.
Příklady
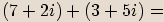

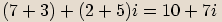

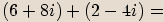

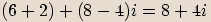

Definice
Součin dvou komplexních čísel
Máme-li dvě komplexní čísla 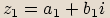 a
a 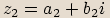 , pak jejich
součinem budeme nazývat komplexní číslo
, pak jejich
součinem budeme nazývat komplexní číslo 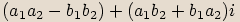 .
Tento součin označujeme
.
Tento součin označujeme  .
.

znát zpaměti. Lze ho odvodit podle pravidel pro násobení dvojčlenů,
přičemž použijeme
 .
. Poznámka
Součin nuly a libovolného komplexního čísla je roven nule.
Poznámka
Pro každá dvě komplexní čísla 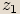 ,
, 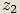 platí, že
platí, že 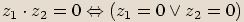 .
.
Příklady


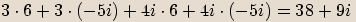

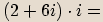

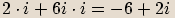

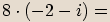

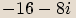

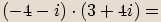

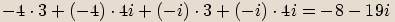

Reciproké číslo
Definice
Reciproká čísla
Číslem převráceným neboli reciprokým ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 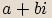 nazýváme komplexní číslo
nazýváme komplexní číslo 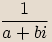 ,
značíme ho
,
značíme ho  .
.
Poznámka
Mějme komplexní číslo 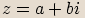 . Pak algebraický tvar komplexního čísla
. Pak algebraický tvar komplexního čísla  dostaneme,
rozšíříme-li zlomek
dostaneme,
rozšíříme-li zlomek  číslem
číslem 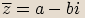 :
:
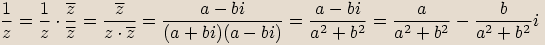
Příklady
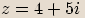

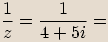

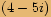 .
. 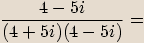

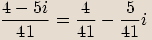

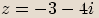

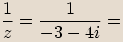
 Zlomek rozšíříme výrazem
Zlomek rozšíříme výrazem 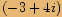 .
.
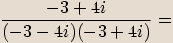

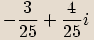



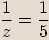

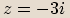

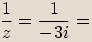

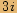 .
.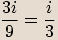

Odčítání a dělení komplexních čísel v algebraickém tvaru
Definice
Rozdíl dvou komplexních čísel
Máme-li dvě komplexní čísla 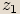 a
a 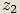 , pak jejich
rozdílem budeme nazývat komplexní číslo
, pak jejich
rozdílem budeme nazývat komplexní číslo 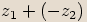 .
Tento rozdíl označujeme
.
Tento rozdíl označujeme  .
.

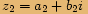 od čísla
od čísla 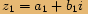 znamená
znamenápřičíst k číslu
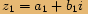 číslo opačné k číslu
číslo opačné k číslu 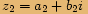 .
. 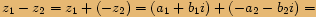
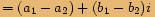
Příklady
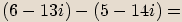

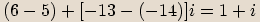

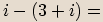

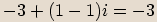

Definice
Podíl dvou komplexních čísel
Máme-li dvě komplexní čísla 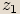 a
a 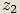 , pak jejich
podílem budeme nazývat komplexní číslo
, pak jejich
podílem budeme nazývat komplexní číslo 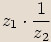 .
Tento podíl označujeme
.
Tento podíl označujeme 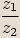 .
.

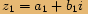 číslem
číslem 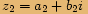 znamená násobit
znamená násobitčíslo
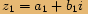 číslem převráceným k číslu
číslem převráceným k číslu 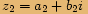 .
.Chceme-li vynásobit
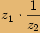 ,
musíme rozšířit zlomek
,
musíme rozšířit zlomek
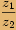 číslem
číslem 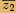 ,
,tedy
 .
.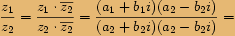
Příklady
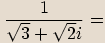
 Rozšíříme zlomek výrazem
Rozšíříme zlomek výrazem  .
.
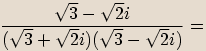

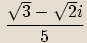

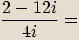
 Rozšíříme zlomek výrazem
Rozšíříme zlomek výrazem 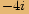 .
.
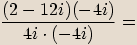

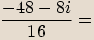

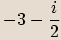

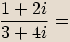
 Rozšíříme zlomek výrazem
Rozšíříme zlomek výrazem 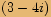 .
.
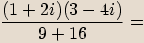

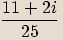

Věta
Pro libovolná komplexní čísla 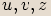 platí následující vlastnosti:
platí následující vlastnosti:
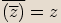

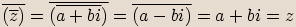



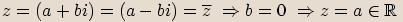
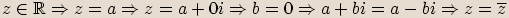


 Označíme
Označíme 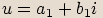 ,
, 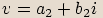 .
.
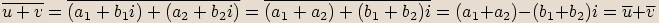
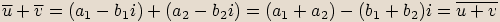


 Označíme
Označíme 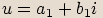 ,
, 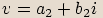 .
.
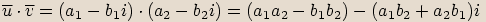
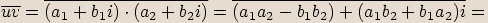
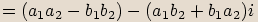


 Označíme
Označíme 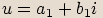 ,
, 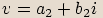 .
.
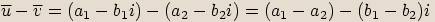
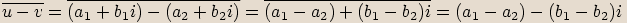

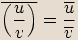
 Označíme
Označíme 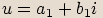 ,
, 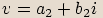 .
.
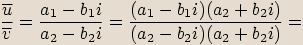
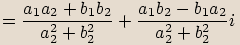
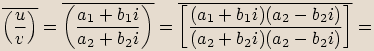
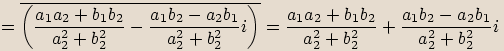

Věta
Pro libovolné komplexní číslo  platí
následující vlastnosti:
platí
následující vlastnosti:
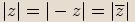

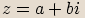
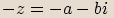
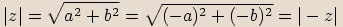
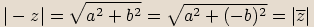

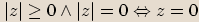

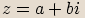
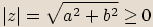 , protože součet dvou nezáporných
reálných čísel je číslo nezáporné a odmocnina z nezáporného čísla je také číslo nezáporné.
, protože součet dvou nezáporných
reálných čísel je číslo nezáporné a odmocnina z nezáporného čísla je také číslo nezáporné. 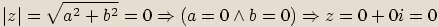
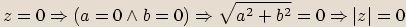



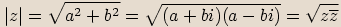

Věta
Pro libovolná dvě komplexní čísla 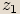 ,
, 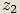 platí:
platí:
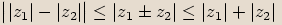
 Body
Body 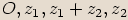 jsou vrcholy rovnoběžníku v Gaussově rovině.
jsou vrcholy rovnoběžníku v Gaussově rovině.
a) Z trojúhelníkové nerovnosti pro trojúhelník s vrcholy
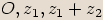 vyplývá, že
vyplývá, že 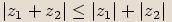 .
. Z trojúhelníkové nerovnosti pro trojúhelník s vrcholy
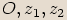 vyplývá, že
vyplývá, že 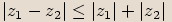 .
. b) Protože trojúhelníková nerovnost pro trojúhelník s vrcholy
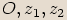 platí pro všechny strany v trojúhelníku, lze dále napsat,
že
platí pro všechny strany v trojúhelníku, lze dále napsat,
že 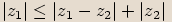 a
a 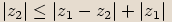 .
Jednoduchou úpravou obou nerovností dostáváme, že
.
Jednoduchou úpravou obou nerovností dostáváme, že  a
a  . Čísla
. Čísla  a
a  jsou navzájem opačná. Protože jsou obě menší nebo rovna číslu
jsou navzájem opačná. Protože jsou obě menší nebo rovna číslu  ,
je menší nebo rovna číslu
,
je menší nebo rovna číslu  i jejich absolutní hodnota.
Platí tedy, že
i jejich absolutní hodnota.
Platí tedy, že 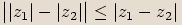 .
.Uvažujeme-li čísla
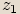 ,
, 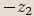 , dostaneme obdobným postupem
, dostaneme obdobným postupem 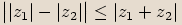 .
. Spojením kroků a) a b) dostáváme, že platí
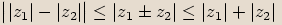 .
.

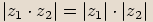

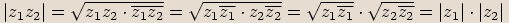

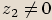 , platí
, platí 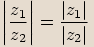

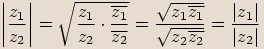
 >>další stránka<<>>nahoru<<
>>další stránka<<>>nahoru<<