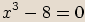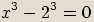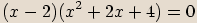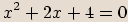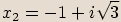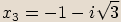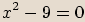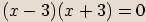Kvadratická rovnice s reálnými koeficienty
Řešit kvadratickou rovnici 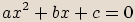 s reálnými koeficienty, kde
s reálnými koeficienty, kde 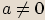 , pokud má nezáporný diskriminant, už umíme
z doby, kdy se probíralo téma rovnice.
, pokud má nezáporný diskriminant, už umíme
z doby, kdy se probíralo téma rovnice.
Tehdy jsme kořeny počítali podle vztahu 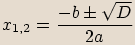 .
.
Nyní se budeme zabývat případem, kdy je diskriminant záporný. Rovnice má opět dva různé kořeny. Ale protože je diskriminant záporné číslo, nelze z něho v oboru reálných čísel vyjádřit odmocninu.
Řešíme-li kvadratickou rovnici v oboru komplexních čísel, postupujeme takto.
Záporné číslo 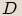 zapíšeme jako
zapíšeme jako  . Rovnost
. Rovnost 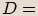
 platí,
protože
platí,
protože 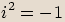 . Číslo
. Číslo 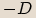 je nezáporné, takže z něho
už lze počítat druhou odmocninu. To znamená, že kořeny rovnice získáme
je nezáporné, takže z něho
už lze počítat druhou odmocninu. To znamená, že kořeny rovnice získáme
ze vztahu 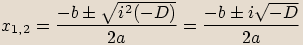 .
.
Jak vidíme ze znamének u imaginaráních složek, tyto dva kořeny jsou navzájem komplexně sdružená imaginární čísla.
Výše uvedené poznatky lze shrnout do následující věty.
Věta
Kvadratická rovnice 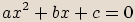 s reálnými koeficienty, kde
s reálnými koeficienty, kde 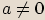 ,
,
a záporným diskriminantem 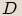 má v oboru komplexních čísel právě dva kořeny,
má v oboru komplexních čísel právě dva kořeny,
a to sdružená imaginární čísla 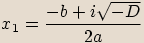 ,
, 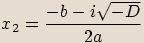 .
.
 Vyplývá z poznámky před větou.
Vyplývá z poznámky před větou.
Poznámka
V oboru komplexních čísel má tedy každá kvadratická rovnice s reálnými koeficienty řešení.
Příklady
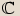 rovnice:
rovnice:
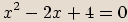

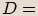

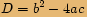
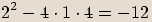
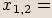

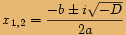
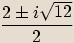

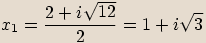

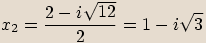

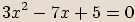

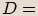

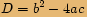
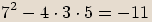
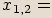

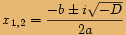
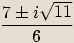

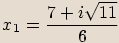

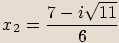

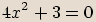

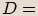

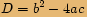

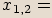

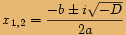
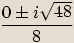

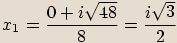

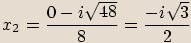

Poznámka
Kromě kvadratických rovnic s reálnými koeficienty existují také kvadratické rovnice s koeficienty komplexními. Toto téma je však nad rámec našeho učiva, a proto se ním nebudeme podrobněji zabývat. K jeho nastudování je možné použít knihu [1] z přehledu použité literatury.
>>nahoru<<Binomická rovnice
Definice
Binomickou rovnicí s neznámou 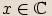 nazveme každou rovnici tvaru
nazveme každou rovnici tvaru 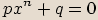 , kde
, kde 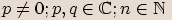 .
.
Každou binomickou rovnici lze upravit na tvar 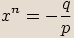 . Řešit takovou rovnici pak znamená
určit všechny
. Řešit takovou rovnici pak znamená
určit všechny 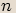 -té odmocniny z čísla
-té odmocniny z čísla 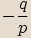 . Označíme
. Označíme 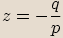 .
.
Je-li tedy 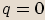 , pak i
, pak i 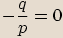 a rovnice má právě jedno řešení
a rovnice má právě jedno řešení  .
.
Je-li 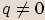 a
a  , pak rovnice má
, pak rovnice má 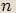 různých komplexních kořenů, a to
různých komplexních kořenů, a to 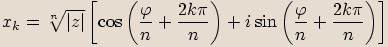 , kde
, kde 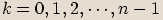 .
.
Tyto kořeny jsou vrcholy pravidelného 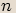 -úhelníka se středem v počátku a poloměrem kružnice opsané
-úhelníka se středem v počátku a poloměrem kružnice opsané 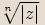 .
.
Podrobnější odvození kořenů rovnice 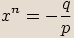 bylo uvedeno v
kapitole
bylo uvedeno v
kapitole
n-tá odmocnina z komplexního čísla.
Příklady
 rovnice:
rovnice:
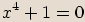

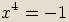

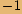 zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.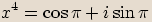

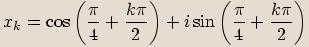 , kde
, kde 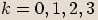

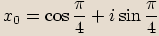

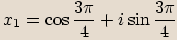

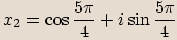

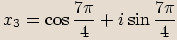

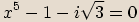

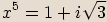

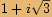 zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.
zapíšeme v goniometrickém tvaru a spočítáme všechna řešení rovnice.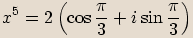

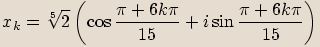 , kde
, kde 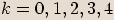

Poznámka
Binomickou rovnici 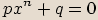 , kde
, kde 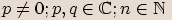 ,
lze také řešit pomocí rozkladu levé strany
na součin mnohočlenů.
,
lze také řešit pomocí rozkladu levé strany
na součin mnohočlenů.
Při tomto postupu nejprve obě strany
rovnice vydělíme číslem 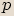 a poté rozložíme levou
stranu na součin mnohočlenů nižších stupňů. Dále využijeme vlastnosti součinu,
že součin je roven nule, pokud je roven nule alespoň jeden z činitelů. Položíme všechny mnohočleny rovny nule
a z takto vzniklých dílčích rovnic dopočítáme všechna řešení původní rovnice.
a poté rozložíme levou
stranu na součin mnohočlenů nižších stupňů. Dále využijeme vlastnosti součinu,
že součin je roven nule, pokud je roven nule alespoň jeden z činitelů. Položíme všechny mnohočleny rovny nule
a z takto vzniklých dílčích rovnic dopočítáme všechna řešení původní rovnice.
Při rozkladu levé strany se často používají vzorce
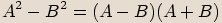 ,
,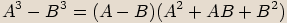 ,
,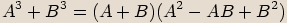 ,
,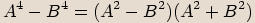 .
.Příklady
 rovnice:
rovnice:
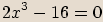

 .
.