Vzájemná poloha přímky a roviny

Ve stereometrii rozlišujeme tři různé vzájemné polohy přímky a roviny. Říkáme, že nemá-li přímka s rovinou žádný společný bod, pak je přímka s danou rovinou rovnoběžná. Má li přímka s rovinou společný právě jeden bod, pak je přímka různoběžná s rovinou, jejich společný bod nazýváme průsečíkem.
Má li přímka s rovinou společné alespoň dva body, pak tato přímka leží v dané rovině. Všechny body přímky jsou zároveň i body roviny.

Pouze na základě definice nelze určit, zda je přímka s rovinou rovnoběžná, proto musíme zavést kriterium rovnoběžnosti.

Kritérium rovnoběžnosti přímky a roviny

Přímka p je rovnoběžná s rovinou α, obsahuje-li rovina α alespoň jednu přímku q, která je s přímkou p rovnoběžná.

V případě různoběžnosti přímky a roviny potřebujeme nalézt průsečík, tj. určit průnik přímky s rovinou. Pro nalezení průsečíku se využívá následující postup.

Průnik přímky s rovinou

Při konstrukci průniku dané přímky p s danou rovinou α, přímka je s rovinou různoběžná, se používá tento obecný postup:

přímkou p se vhodně proloží pomocná rovina β různoběžná s α
sestrojí se průnik roviny α s rovinou β, průnikem je přímka q (Kapitola 5.3)
průnik přímky p s přímkou q je pak hledaným průnikem přímky p a roviny α

Vzájemná poloha	Společné body	Číslo obrázku	Značení
Přímka leží v rovině	všechny body přímky	obr. 1	p 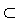α
Rovnoběžné různé	žádné	obr. 2	p \|\| α
Různoběžné	jeden	obr. 3	p α

Obr. 1	Přímka leží v rovině, má s ní společné všechny body.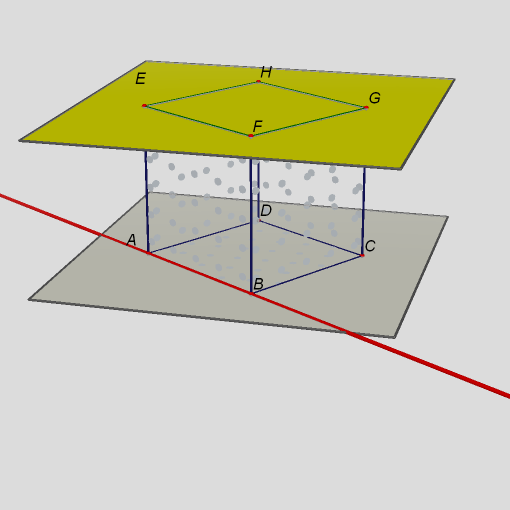
Obr. 2	Přímka a rovina jsou rovnoběžné. Přímka je rovnoběžná s rovinou, je-li rovnoběžná s alespoň jednou její přímkou (např. EF).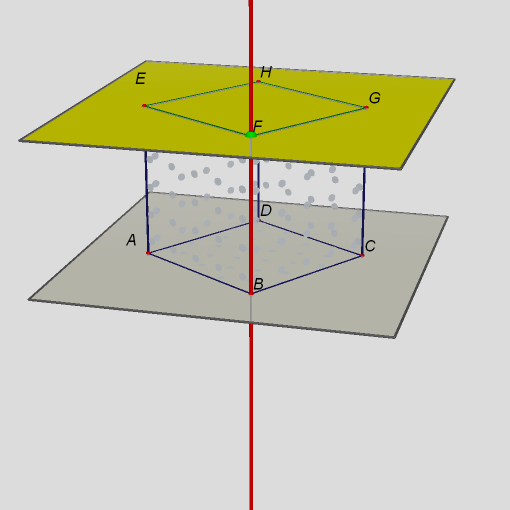
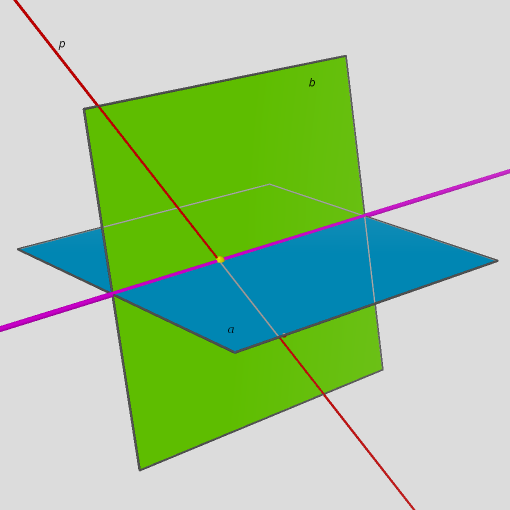
Obr. 3	Přímka a rovina jsou různoběžné, mají jeden společný bod, který nazýváme průsečík.

Úlohy

1. Máme dánu krychli ABCDEFGH. Určete všechny přímky které prochází bodem A a dalším vrcholem krychle a jsou rovnoběžné s rovinou horní podstavy.

Řešením jsou přímky AB, AC a AD.

Skryj výsledek

Zobraz výsledek

2. Máme dánu krychli ABCDEFGH. Určete všechny roviny procházející bodem B a dalšími dvěma vrcholy krychle, které jsou různoběžné s přímkou FG.

Jsou to roviny ABF, BDH, BGH.

Skryj výsledek

Zobraz výsledek

3. Máme dánu krychli ABCDEFGH. Určete všechny roviny procházející bodem B a dalšími dvěma vrcholy krychle, které jsou rovnoběžné různé s přímkou FG.

Řešením jsou pouze roviny ABC a BEH.

Skryj výsledek

Zobraz výsledek

4. Máme dánu krychli ABCDEFGH. Určete vzájemnou polohu přímky AC s rovinou DBF a v případě různoběžnosti určete jejich průsečík.

Přímka je s rovinou různoběžná, průsečík je střed čtverce ABCD.

Skryj výsledek

Zobraz výsledek

5. Máme dán pravidelný čtyřboký jehlan ABCDV. Bod K je střed hrany AB. Určete vzájemnou polohu přímky AC s rovinou KBV a v případě různoběžnosti určete jejich průsečík.

Přímka je s rovinou různoběžná, průsečík je vrchol A.

Skryj výsledek

Zobraz výsledek

6. Máme dán pravidelný čtyřboký jehlan ABCDV. Body K,L,M jsou po řadě středy hran AB, CV, DV. Určete vzájemnou polohu přímky LM s rovinou KCD a v případě různoběžnosti určete jejich průsečík.

Přímka je s rovinou rovnoběžná (kriterium rovnoběžnosti přímky a roviny).

Skryj výsledek

Zobraz výsledek

7. Je dán čtyřstěn ABCV a body L,M,N,P jsou po řadě středy hran AB, BC, AV, BV. Rozhodněte o vzájemné poloze přímky LM s rovinou NPV.

Přímka je s rovinou různoběžná, společný bod je bod L.

Skryj výsledek

Zobraz výsledek

8. Sestrojte průsečík roviny ABG s přímkou FD na krychli ABCDEFGH.

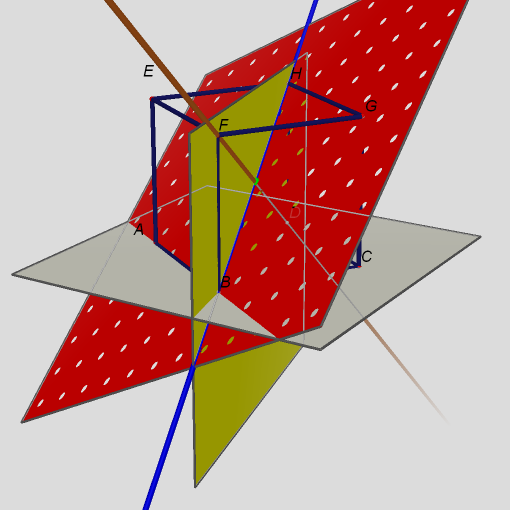
Sestrojíme rovinu ABG a přímku FD. Přímkou FD proložíme pomocnou rovinu BDH. Určíme průsečnici roviny ABG s rovinou BDH, což je přímka BH. Přímky se protínají v jednom bodě, který je společným bodem roviny ABG s přímkou FD.

Skryj výsledek

Zobraz výsledek

9. Je dán pravidelný čtyřboký jehlan ABCDV. Sestrojte průsečík roviny určené vrcholem V, středem hrany BC a středem hrany AD, s přímkou BM, je-li bod M střed hrany DV.

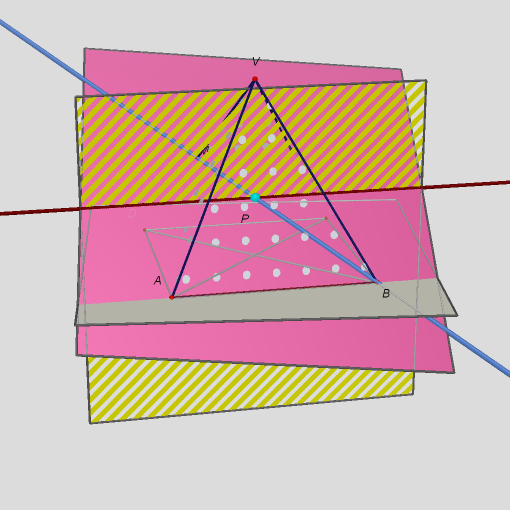
Sestrojíme na jehlanu danou rovinu procházející vrcholem V a přímku BM. Přímkou proložíme rovinu BAM. Obě roviny mají společnou přímku, jejíž průsečík s přímkou BM je hledaný bod P.

Skryj výsledek

Zobraz výsledek

10. Je dán kvádr ABCDEFGH. Určete průnik roviny EFH s přímkou AX, kde bod X leží na polopřímce CG za bodem G.

Rovina EFH je rovinou horní podstavy kvádru. Přímka AX je s touto rovinou různoběžná. Přímkou proložíme rovinu procházející vrcholem F. Společná přímka této roviny a roviny horní podstavy kvádru má s přímkou AX společný jeden bod. Je to právě hledaný průsečík bod P.

Skryj výsledek

Zobraz výsledek