Definice
Definice hyperboly
Definice: Nechť jsou v rovině E_2 dány dva různé body F_1 a F_2 a konstanta a > 0, pro kterou platí 2a<|F_1F_2|.
Hyperbolou k_h budeme rozumět množinu všech bodů v rovině E_2, které mají konstantní absolutní hodnotu rozdílu vzdáleností od bodů F_1 a F_2 rovnu 2a.
k_h= \{ X \in E_2; \, ||F_1X| - |XF_2||=2a, \, kde \; 2a<|F_1F_2|\}.
Pozn.: Kdyby v definici místo "... mají konstantní absolutní hodnotu rozdílu..." bylo jen "... mají konstantní rozdíl...", pak bychom připustili i zápornou vzdálenost, což je prakticky nemožné.
Pokud bychom připustili i případ kdy a=0, mezi hyperboly bychom řadili i osu souměrnosti úsečky F_1F_2.
Kdybychom nezdůraznili, že body F_1 a F_2 jsou různé, připouštěli bychom i případ, kdy body splynou. V takovém případě by 2a mohlo být rovno pouze nule a definici by vyhovovaly všechny body roviny.
Kdyby v definici hyperboly nebylo řečeno "2a<|F_1F_2|", pak bychom připustili, že rozdíl by mohl být buď roven nebo větší než |F_1F_2|. V prvním případě bychom dostali přímku F_1F_2, z níž jsou vyňaty vnitřní body úsečky F_1F_2. V druhém případě by neexistoval žádný bod vyhovující daným podmínkám.
Pokud budete v apletu H1.1 pohybovat bodem X po hyperbole, můžete se přesvědčit, že absolutní hodnota rozdílu vzdáleností bodu X od pevně zvolených bodů F_1 a F_2 je opravdu konstantní. Absolutní hodnota rozdílu těchto vzdáleností je počítána v tabulce vlevo.
Aplet H1.1: Definice hyperboly - konstantní absolutní hodnota rozdílu průvodičů
Základní pojmy
Nyní vymezíme několik důležitých pojmů vztahujících se k hyperbole. V dalším textu budou termíny používány.
Body F_1 a F_2 nazýváme ohniska hyperboly nebo někdy také fokusy. Z definice tedy plyne, že každá hyperbola stejně jako elipsa má dvě ohniska, dva různé pevně dané body. Vzdálenosti |F_1X|, |F_2X|, nebo také spojnice F_1X, F_2X libovolného bodu X \in k_h a ohnisek se nazývají průvodiče bodu X.
Přímku F_1F_2 budeme značit o_1. Jedná se o hlavní osu hyperboly. Přímka kolmá na hlavní osu o_1 procházející bodem S, který je středem úsečky F_1F_2, se nazývá vedlejší osa hyperboly a značí se o_2. Bod S je zároveň středem hyperboly.
Body A, B, které jsou průsečíky hlavní osy o_1 a hyperboly, se nazývají vrcholy hyperboly.
Podle definice platí, že absolutní hodnota rozdílu průvodičů libovolného bodu hyperboly je rovna konstantě 2a > 0. Tedy pro každý bod M hyperboly platí buď F_1M - F_2M = 2a a to v případě, že je |F_1M| > |F_2M|. Nebo platí F_2M - F_1M = 2a v případě, že je |F_2M| > |F_1M|. Znamená to, že hyperbola je složena ze dvou disjunktních částí (nemají žádný společný bod), jimž říkáme větve hyperboly. Větve hyperboly se neomezeně blíží ke dvěma přímkám u_1, u_2, které procházejí středem hyperboly. Jsou to asymptoty hyperboly. Mají tu speciální vlastnost, že se směrem od středu S čím dál více blíží větvím hyperboly, ale nikdy se jich "nedotknou". V projektivním rozšíření eukleidovského prostoru bychom mohli říci, že to jsou tečny hyperboly v bodě, který je nekonečně vzdálený a přesto na hyperbole leží; tečny v tzv. nevlastním bodě.
Platí-li vztah z definice pro každý bod ležící na hyperbole, musí pak platit i pro vrcholy A, B. Tudíž platí následující rovnosti:
| |AF_1| - |AF_2| | = | |BF_1| - |BF_2| | = 2a
|AF_2| = |AB| + |BF_2| = |BA| + |AF_1| = |BF_1|
2a = | |AF_1| - |AF_2| | = | |AF_1| - ( |AB| + |BF_2| ) | = | |AF_1| - |AB| - |AF_2| | = |AB|
Tedy:
2a = |AB|
a = |AS| = |SB|.
Z předchozích rovnic vyplývá, že konstanta a představuje délku úsečky AS či SB. Konstantu a budeme nazývat délka hlavní poloosy.
Zřejmě, pokud existuje délka hlavní poloosy, očekáváme i konstantu, která bude vyjadřovat délku vedlejší poloosy stejně tak, jak tomu je u elipsy. Ovšem hyperbola nemá žádné vedlejší vrcholy (žádné body ležící na o_2), protože všechny body vedlejší osy o_2 mají rozdíl průvodičů roven nule. I přesto je zde zavedená konstanta b - délka vedlejší poloosy. Vyjadřuje délku úsečky AU_1 (resp. B U_2), kde bod U_1 (resp. U_2) je jeden z průsečíků asymptoty a přímky kolmé na hlavní osu o_1 procházejících vrcholem A (resp. B). Platí b = |AU_1| = |BU_2|.
Další důležitou konstantou je tzv. excentricita, neboli výstřednost. Značí se e a určuje vzdálenost ohniska od středu elipsy. Vyjadřuje tedy délku úsečky F_1S či F_2S.
Všechny výše uvedené konstanty, body a přímky jsou vyznačené na obrázku H1.1.
Obrázek H1.1: Hyperbola
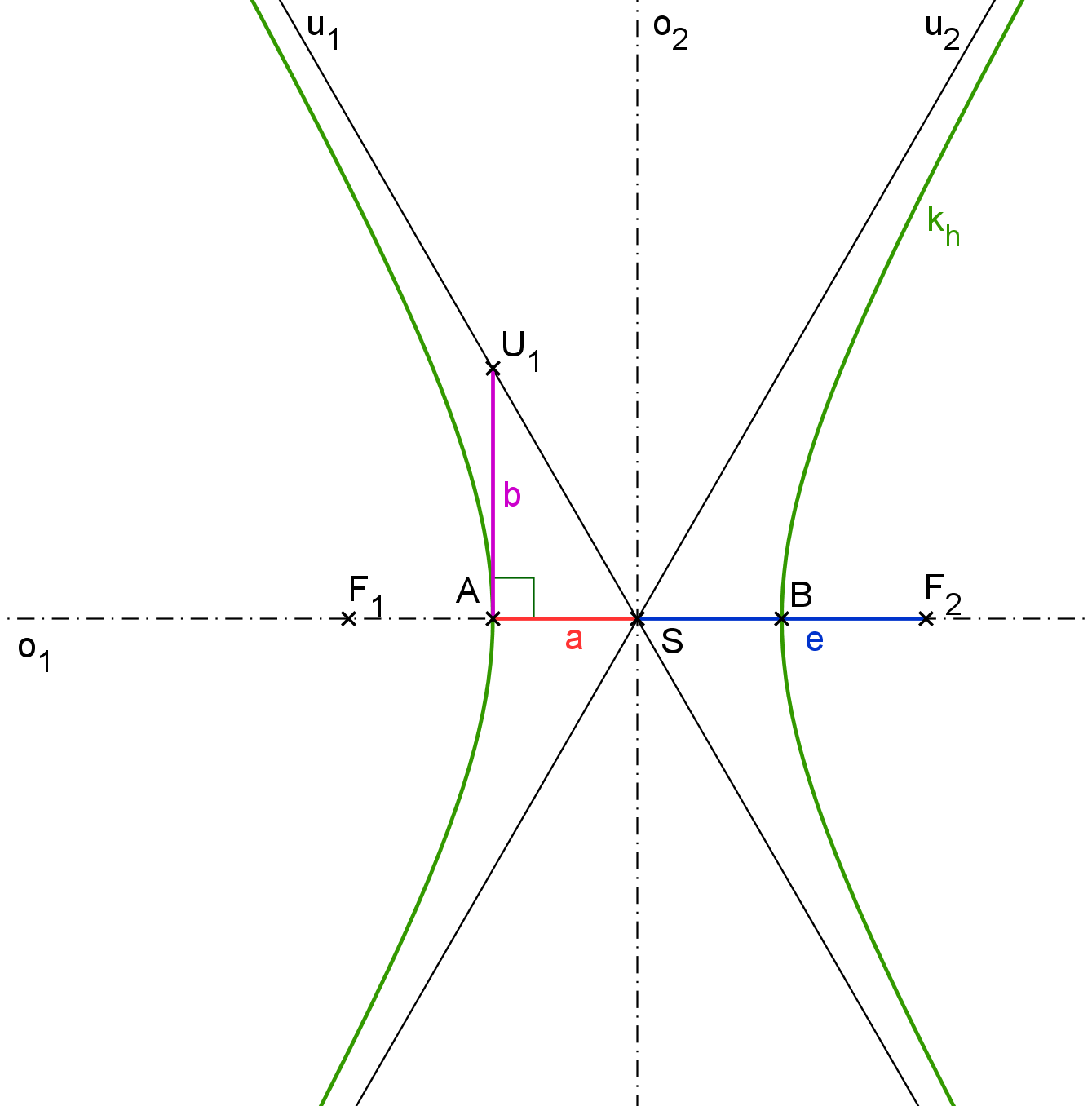
Pro větší přehlednost a ucelenost termínů je zde tabulka, která shrnuje všechny pojmy:
| označení | název | definice |
|---|---|---|
| k_h | hyperbola | |
| F_1, F_2 | ohniska (fokusy) | |
| A, B | vrcholy hyperboly | průsečíky o_1 a k_h |
| S | střed hyperboly | střed úsečky F_1F_2 |
| o_1 | hlavní osa | přímka AB |
| o_2 | vedlejší osa | přímka kolmá na o_1 a procházející S |
| u_1, u_2 | asymptoty | tečny hyperboly v nevlastním bodě |
| a | délka hlavní poloosy | |AS| či |SB| |
| b | délka vedlejší poloosy | |AU_1| či |BU_2| |
| e | excentricita (výstřednost) | |F_1S| či |SF_2| |