Goniometrické rovnice
V tejto časti si uvedieme rôzne metódy riešenia goniometrických rovníc. Každá časť obsahuje vzorové riešené príklady a zároveň veľa úloh k precvičovaniu, ktoré sú obohatené riešením.
Základné goniometrické rovnice
Riešenie základných goniometrických rovníc je viditeľné priamo z grafov goniometrických rovníc a z tabuľkových hodnôt, ako si to môžeme pozrieť na úvodných vzorovo vyriešených príkladoch. Úlohy venovane základným goniometrickým rovniciam sú doprevadzané riešenim, poprípade návodmi, ktoré sa zobrazí po kliknutí na prislušný príklad.
Poznámka: Pokiaľ argument x predstavuje veľkosť uhla, môžme výsledok vyjadriť tiež v oblúkovej alebo v stupňovej miere, napríklad ![]()
Príklad 1
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Riešenie je vidieť priamo z grafu funkcie sínus: 
Pri pohľade na graf funkcie sínus je vidieť, že pre ![]() je na danom intervale
je na danom intervale ![]() funckia
funckia ![]() .
.
Využitím periody ![]() dostávame množinu riešeni
dostávame množinu riešeni ![]() .
.
Príklad 2
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Pri riešeni využijeme graf funkcie kosínus a zistíme, v ktorých hodnotách kosínus nadobúda hodnoty 0.

Pri pohľade na graf funkcie kosínus je vidieť, že pre ![]() ,
, ![]() ,
, ![]() a
a ![]() je na intervale
je na intervale ![]() funkcia
funkcia ![]() . Využitim periodičnosti funkcie kosínus, podobne ako v prvom príklade, dostávame riešenie rovnice v tvare
. Využitim periodičnosti funkcie kosínus, podobne ako v prvom príklade, dostávame riešenie rovnice v tvare
Pre návrat na začiatok stlač => hore
Príklad 3
Riešte goniometrickú rovnicu s neznámou ![]() a výsledok zapíšte v stupňovej miere:
a výsledok zapíšte v stupňovej miere:
Riešenie
Riešenie tejto úlohy je opäť viditeľné priamo z grafu funkcie sínus a z tabuľkových hodnôt funkcie sínus:

Platí, že pre ![]() je riešením
je riešením ![]() , pre
, pre ![]() je riešením
je riešením ![]() .
.
Funkcia kosínus je periodická s periódou ![]() , obecné riešenie je teda
, obecné riešenie je teda ![]() a výsledok v stupňovej miere je
a výsledok v stupňovej miere je ![]() .
.
Príklad 4
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Poznámka: Funkčné hodnoty uvádzame na 4 desatinné miesta.
Riešenie
Použitím kalkulačky alebo matematických tabuliek pre kosínus uhla v oblúkovej miere dostávame riešenie ![]() a
a ![]() , kde
, kde ![]()
Použitím matematických tabuliek kosínusu uhla v stupňovej miere dostávame riešenia ![]() a
a ![]()
Výsledné riešenie zapíšeme v tvare ![]()
Pre návrat na začiatok stlač => hore
Úlohy
Riešte rovnice s neznámou ![]() :
:
a) 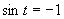
 Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
Z grafu a z tabuľkových hodnôt plynie, že riešením je množina 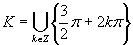 .
.
b) 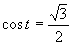
 Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
Z grafu a z tabuľkových hodnôt plynie, že riešením je množina 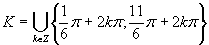 .
.
c) 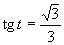
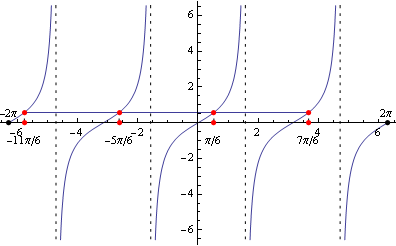 Z grafu a z tabuľkových hodnôt plynie, že riešením je množina
Z grafu a z tabuľkových hodnôt plynie, že riešením je množina 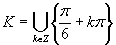 .
.
d) 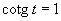
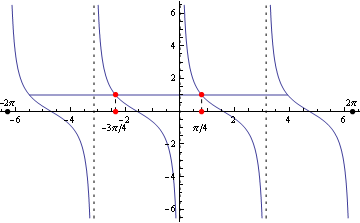 Riešením je množina
Riešením je množina 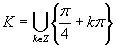 .
.
e) 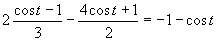
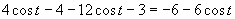
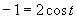
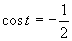
 Z grafu plynie, že riešením je množina
Z grafu plynie, že riešením je množina 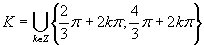 .
.
f) Riešte rovnicu s neznámou t a výsledok zapíšte v stupňovej miere s presnosťou na minúty: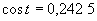 Riešením je množina
Riešením je množina 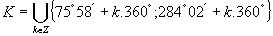 .
.
g) Riešte rovnicu s neznámou t na intervale ![]() a výsledok zapíšte v oblúkovej miere s presnosťou na dve desatinné miesta:
a výsledok zapíšte v oblúkovej miere s presnosťou na dve desatinné miesta: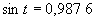 Výsledkom je množina
Výsledkom je množina 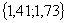 .
.
Pre návrat na začiatok stlač => hore
Zložitejšie goniometrické rovnice
Substitúcia na základný typ
Pomocou jednoduchej substitúcie ![]() alebo
alebo ![]() prevedieme zložitejšiu goniometrickú rovnicu typu
prevedieme zložitejšiu goniometrickú rovnicu typu ![]() alebo
alebo ![]() , kde g je goniometrická funkcia s neznámou x a l, k sú reálne čísla, na základný typ goniometrických rovníc
, kde g je goniometrická funkcia s neznámou x a l, k sú reálne čísla, na základný typ goniometrických rovníc ![]() .
.
Príklad 1
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Zavedieme pomocnú substitúciu ![]() a dostaneme rovnicu
a dostaneme rovnicu ![]() .
.

Z grafu je vidieť, že pre ![]() je na intervale
je na intervale ![]() funkcia
funkcia ![]() .
.
Využitím periodičnosti funkcie sínus dostávame riešenia
![]() , a
, a ![]() .
.
Vrátime sa k substitúcií a postupnou úpravou dostávame:
![]()
![]()
![]() (Prvé riešenie.)
(Prvé riešenie.)
![]()
![]()
![]() (Druhé riešenie.)
(Druhé riešenie.)
Výsledné riešenie môžme zapísať v tvare ![]() .
.
Príklad 2
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Platí podmienka: ![]()
Zavedieme substitúciu ![]() a dostávame rovnicu
a dostávame rovnicu ![]() .
.
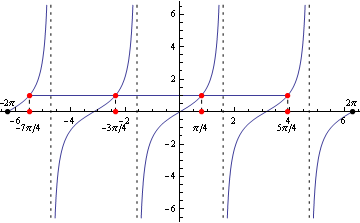
Z grafu a zo základných tabuľkových hodnôt funkcie tangens plynie, že pre ![]() .
.
Vrátime sa späť k substitúcii a postupnou úpravou dostávame:
![]()
![]()
![]()
![]()
Výsledok zapíšeme v tvare ![]() .
.
Pre návrat na začiatok stlač => hore
Úlohy
Riešte rovnice s neznámou ![]() :
:
a)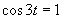 Zavedieme substitúciu
Zavedieme substitúciu 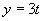
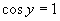
 Z grafu a zo základných tabuľkových hodnôt funkcie kosínus plynie, že
Z grafu a zo základných tabuľkových hodnôt funkcie kosínus plynie, že 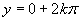 .
Vrátime sa k substitúcii a postupnou úpravou dostávame
.
Vrátime sa k substitúcii a postupnou úpravou dostávame 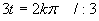
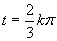 .
Výsledným riešením je množina
.
Výsledným riešením je množina 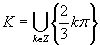 .
.
b)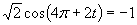
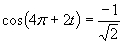
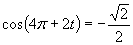 Zavedieme substitúciu
Zavedieme substitúciu 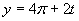 .
.
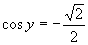
 Z grafu je vidieť, že
Z grafu je vidieť, že 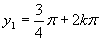 a
a 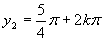 .
Vrátime sa k substitúcii a v prvom prípade dostávame
.
Vrátime sa k substitúcii a v prvom prípade dostávame 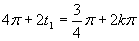
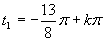 (prvé riešenie)
V druhom prípade platí:
(prvé riešenie)
V druhom prípade platí: 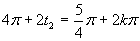
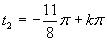 (druhé riešenie)
Výslednú množinu zapíšeme v tvare
(druhé riešenie)
Výslednú množinu zapíšeme v tvare 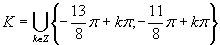 .
.
c)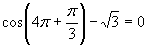 Zavedieme substitúciu
Zavedieme substitúciu 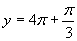 .
.
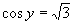 Také y neexistuje, takže môžme písať
Také y neexistuje, takže môžme písať 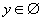 .
.
d)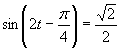 Zavedieme substitúciu
Zavedieme substitúciu 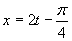 .
.
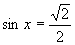
 Z grafu a zo základných tabuľkových hodnôt funckie sínus plynie
Z grafu a zo základných tabuľkových hodnôt funckie sínus plynie 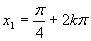 a
a 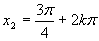 .
Vrátime sa k substitúcii
.
Vrátime sa k substitúcii 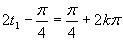
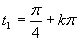
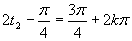
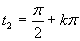 Výsledným riešením je množina
Výsledným riešením je množina 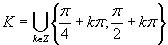 .
.
e)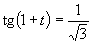
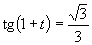 Zavedieme substitúciu
Zavedieme substitúciu 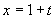
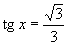
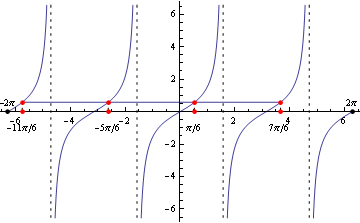 Z grafu a zo základných tabuľkových hodnôt funckie tangens plynie:
Z grafu a zo základných tabuľkových hodnôt funckie tangens plynie: 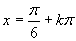 Vrátime sa k substitúcii a úpravou postupne dostávame:
Vrátime sa k substitúcii a úpravou postupne dostávame: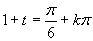
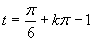 Výsledným riešením je množina
Výsledným riešením je množina 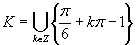 .
.
Pre návrat na začiatok stlač => hore
Substitúcia na kvadratickú rovnicu
Pomocou ďalšiej jednoduchej substitúcie prevedieme zložitejšiu goniometrickú rovnicu, ktorá obsahuje goniometrickú funkciu, v druhej alebo vo štvrtej mocnine, na kvadratickú rovnicu. Pri tomto type úloh často využívame vzorce pre (goniometrické funkcie).
Príklad 1
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Zavedieme substitúciu ![]() .
.
Platí: ![]()
Vypočítame diskriminant kvadratickej rovnice ![]() pomocou známeho vzorca:
pomocou známeho vzorca:
V našom prípade:
Určíme riešenie kvadratickej rovnice pomocou vzorca
Čiže![]() .
.

Vrátime sa k substitúcií ![]() .
.
Platí ![]() , čiže
, čiže![]() .
.
Ďalej ![]() , takže
, takže ![]() (vidno z grafu).
(vidno z grafu).
Riešenie zapíšeme v tvare ![]() .
.
Príklad 2
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Zavedieme substitúciu
![]() .
.
Platí, že ![]() .
.
Vypočítame diskriminant kvadratickej rovnice a určíme riešenia rovnice podobne ako v predchádzajúcom príklade.
![]()
Riešenia kvadratickej rovnice teda sú:

Vrátime sa k substitúcií ![]() .
.
V prvom prípade dostávame ![]()
V druhom prípade je ![]() .
.
(Riešenie je vidieť z grafu a z tabuľkových hodnôt, postupujeme podobne ako v príkladoch predchádzajúcej kapitoly.)
Výsledné riešenie zapíšeme v tvare ![]() .
.
Príklad 3
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Použijeme vzorce ![]() .
.
![]()
Upravíme rovnicu do najjednoduchšieho tvaru s využitím spoločného menovateľa:
![]()
![]() (Použili sme vzorec
(Použili sme vzorec ![]() .)
.)
![]() (Platí, že
(Platí, že ![]()
![]()
![]()
Zavedieme substitúciu ![]() a dostaneme:
a dostaneme:
![]()
Vyriešime kvadratickú rovnicu (vypočítame diskriminant a určíme korene kvadratickej rovnice, vzorce pre výpočet diskriminantu a koreňov kvadratickej rovnice sú uvedené v prvom príklade danej kapitoly).
![]()
![]()
Vrátime sa k substitúcií ![]() a po dosadení za t dostaneme:
a po dosadení za t dostaneme:
![]()

Z grafu a využitím periodičnosti funkcie kosínus dostávame koreň pre ![]() :
:![]()
V druhom prípade dostávame pre ![]() :
:
![]()

![]()
Výsledné riešenie zapíšeme v tvare ![]() .
.
Pre návrat na začiatok stlač => hore
Úlohy
Riešte rovnice s neznámou ![]() :
:
a)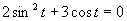
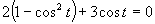 (Používame vzorce uvedené v časti.)
(Používame vzorce uvedené v časti.)
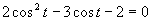 Zavedieme substitúciu
Zavedieme substitúciu 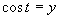 .
.
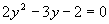 (Vypočítame diskriminant kvadratickej rovnice a určíme riešenia rovnice, postupujeme ako vo vzorových príkladoch tejto kapitoly.)
(Vypočítame diskriminant kvadratickej rovnice a určíme riešenia rovnice, postupujeme ako vo vzorových príkladoch tejto kapitoly.)
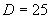
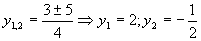 Vrátime sa k substitúcií
Vrátime sa k substitúcií 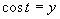 a po dosadení za y dostávame:
a po dosadení za y dostávame:
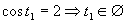

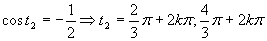 (Využili sme graf a periodičnosť funkcie kosínus.)
Výsledné riešenie napíšeme v tvare
(Využili sme graf a periodičnosť funkcie kosínus.)
Výsledné riešenie napíšeme v tvare 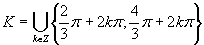 .
.
b)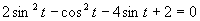
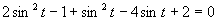 (Používame vzorce uvedené v časti).
(Používame vzorce uvedené v časti).
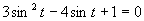 Zavedieme substitúcia
Zavedieme substitúcia 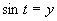 .
.
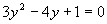
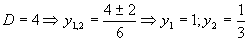
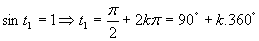 (Výsledok je vidieť z grafu funckie sínus, môžme ho zapísať aj v stupňovej miere).
(Výsledok je vidieť z grafu funckie sínus, môžme ho zapísať aj v stupňovej miere).
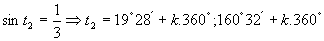 (Z grafu funkcie sínus príslušné hodnoty nevyčítame, preto využíjeme tabuľkové hodnoty a výsledok zapíšeme v stupňovej miere).
Výsledné riešenie napíšeme v tvare
(Z grafu funkcie sínus príslušné hodnoty nevyčítame, preto využíjeme tabuľkové hodnoty a výsledok zapíšeme v stupňovej miere).
Výsledné riešenie napíšeme v tvare 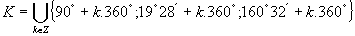 .
.
c)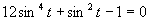 Zavedieme substitúciu
Zavedieme substitúciu 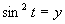 .
.
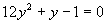
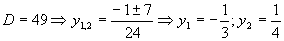
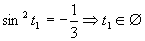 (Druhá mocnina je kladné číslo).
(Druhá mocnina je kladné číslo).
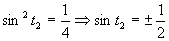

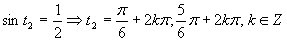
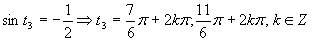 Využitím periodičnosti funkcie sínus dostávame výsledné riešenie, ktoré zapíšeme v tvare
Využitím periodičnosti funkcie sínus dostávame výsledné riešenie, ktoré zapíšeme v tvare 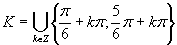 .
.
d)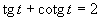
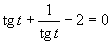 (Používame vzorce uvedené v časti).
Aby výrazy v rovnici boli definované, musí platiť:
(Používame vzorce uvedené v časti).
Aby výrazy v rovnici boli definované, musí platiť: 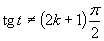
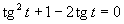 Zavedieme substitúciu
Zavedieme substitúciu 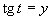 .
.
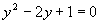 (Vyriešime kvadratickú rovnicu a urćíme korene rovnice).
(Vyriešime kvadratickú rovnicu a urćíme korene rovnice).
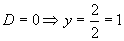
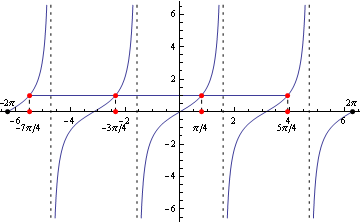
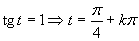 (Využívame periodičnosť funkcie tangens).
Výsledné riešenie napíšeme v tvare
(Využívame periodičnosť funkcie tangens).
Výsledné riešenie napíšeme v tvare 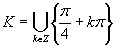 .
.
e)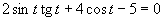
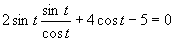 (Použili sme vzorec
(Použili sme vzorec ![]() ).
Aby výrazy v rovnici boli definované, musí platiť:
).
Aby výrazy v rovnici boli definované, musí platiť: 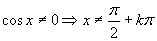
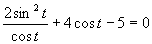
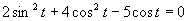
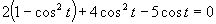 (Používame vzorce uvedené v časti).
(Používame vzorce uvedené v časti).
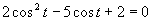 Zavedieme substitúciu
Zavedieme substitúciu 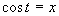 .
.
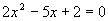 Vyriešime kvadratickú rovnicu (vypočítame diskriminant kvadratickej rovnice a určíme korene rovnice):
Vyriešime kvadratickú rovnicu (vypočítame diskriminant kvadratickej rovnice a určíme korene rovnice): 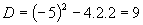
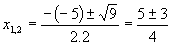
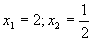 Vrátime sa k substitúcií a pomocou grafu nájdeme korene rovníc.
Vrátime sa k substitúcií a pomocou grafu nájdeme korene rovníc. 
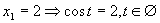 (Také t neexistuje).
(Také t neexistuje).
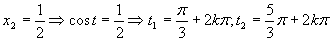 (Využívame periodičnosť funkcie kosínus).
Výsledné riešenie napíšeme v tvare
(Využívame periodičnosť funkcie kosínus).
Výsledné riešenie napíšeme v tvare 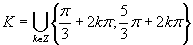 .
.
Pre návrat na začiatok stlač => hore
Dvojnásobný argument
Pri tomto type úloh využívame vzorce pre dvojnásobný uhol, taktiež sa predpokladá znalosť predchádzajúcich typov úloh.
Príklad 1
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule). Odkiaľ plynie: ![]()
Prvá možnosť ![]()

Z grafu a z tabuľkových hodnôt funkcie kosínus plynie, že ![]() .
.
Druhá možnosť ![]()
Úpravou dostávame:
![]()

Z grafu a z tabuľkových hodnôt funkcie kosínus plynie, že ![]() .
.
Výsledné riešenie zapíšeme v tvare
![]() .
.
Príklad 2
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule). ![]()
Prvá možnosť ![]()
![]()

Z grafu a z tabuľkových hodnôt funkcie kosínus plynie, že ![]() .
.
Druhá možnosť ![]()
Úpravou dostávame:
![]()

Z grafu a z tabuľkových hodnôt funkcie kosínus plynie, že ![]() .
.
Výsledné riešenie zapíšeme v tvare
![]() .
.
Príklad 3
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule). ![]()
Prvá možnosť ![]()
Úpravou dostávame:
![]()

Z grafu a z tabuľkových hodnôt funkcie kosínus plynie, že ![]() .
.
Druhá možnosť ![]()
Po úprave dostávame:
![]()

Z grafu plynie, že ![]() .
.
Výsledné riešenie zapíšeme v tvare
Pre návrat na začiatok stlač => hore
Úlohy
Riešte rovnice s neznámou ![]() :
:
a)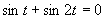
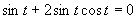 (Používame vzorce pre dvojnásobný argument.)
(Používame vzorce pre dvojnásobný argument.)
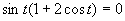 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule.)
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule.)
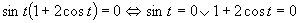
Prvá možnosť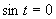

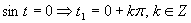 (využitím grafu a tabuľkových hodnôt funkcie sínus)
(využitím grafu a tabuľkových hodnôt funkcie sínus)
Druhá možnosť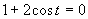
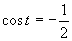

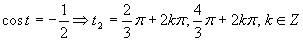 (využitím grafu a tabuľkových hodnôt funkcie kosínus)
(využitím grafu a tabuľkových hodnôt funkcie kosínus)
Výsledné riešenia napíšeme v tvare 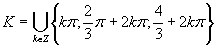 .
.
b)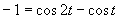
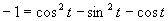 (Používame vzorce pre dvojnásobný argument.)
(Používame vzorce pre dvojnásobný argument.)
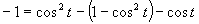
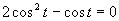
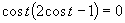
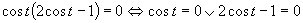 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Prvá možnosť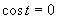

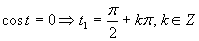
Druhá možnosť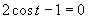
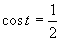

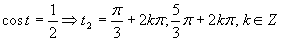
Výsledné riešenie zapíšeme v tvare 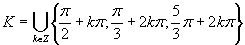 .
.
c)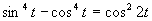
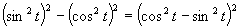 (Používame vzorce pre dvojnásobný argument.)
(Používame vzorce pre dvojnásobný argument.)
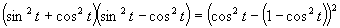 (Použili sme vzorec
(Použili sme vzorec ![]() .)
.)
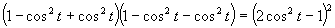
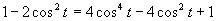
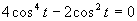
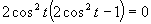
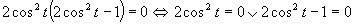 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Prvá možnosť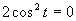
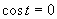

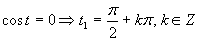
Druhá možnosť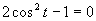
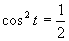
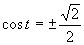

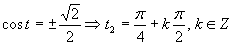
Výsledné riešenia zapíšeme v tvare 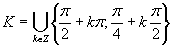 .
.
d)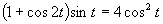
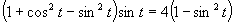 (Používame vzorce pre dvojnásobný argument.)
(Používame vzorce pre dvojnásobný argument.)
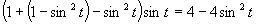
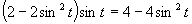
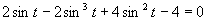
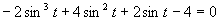
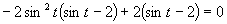
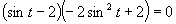
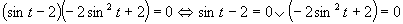 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Prvá možnosť 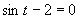
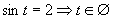 (také t neexistuje)
(také t neexistuje)
Druhá možnosť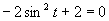
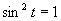
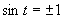

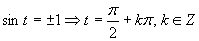
Výsledné riešenie napíšeme v tvare 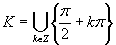 .
.
e)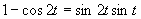
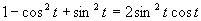 (Používame vzorce pre dvojnásobný argument.)
(Používame vzorce pre dvojnásobný argument.)
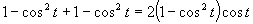
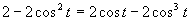
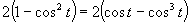
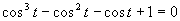
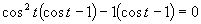
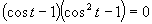
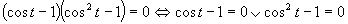 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Prvá možnosť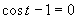
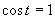

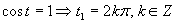
Druhá možnosť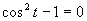
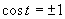

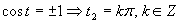 (Zahŕňa v sebe aj prvé riešenie, vplyv periódy.)
(Zahŕňa v sebe aj prvé riešenie, vplyv periódy.)
Výsledné riešenie zapíšeme v tvare 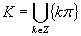 .
.
Pre návrat na začiatok stlač => hore
Súčet a rozdiel goniometrických funkcií, súčtové vzorce
Pri tomto type úloh využívame vzorce pre (súčet a rozdiel goniometrických funkcií, súčtové vzorce). Zároveň sa predpokladá znalosť predchádzajúcich typov úloh.
Príklad 1
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
![]() (Využijeme
(Využijeme ![]() .)
.)
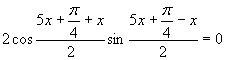 (Použili sme vzorec pre
(Použili sme vzorec pre ![]() .)
.)
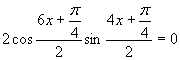
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule). 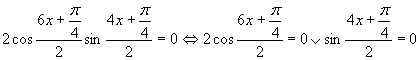
Prvá možnosť
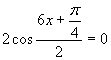
Po úprave dostaneme:
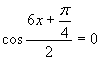
Zavedieme substitúciu:
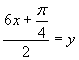
![]()

Vrátime sa k substitúcií a upravíme rovnicu:
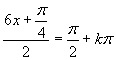
Druhá možnosť

Zavedieme substitúciu:
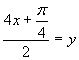
![]()

![]()
Vrátime sa k substitúcií a upravíme rovnicu:
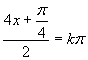
![]()
![]() (Druhé riešenie príkladu.)
(Druhé riešenie príkladu.)
Výsledné riešenie zapíšeme v tvare ![]() .
.
Príklad 2
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
![]()
![]() (Použili sme vzorec pre
(Použili sme vzorec pre ![]() ).
).
![]() .)
.)
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule). ![]()
Prvá možnosť
Zavedieme substitúciu:
![]()

Vrátime sa k substitúcií a upravíme rovnicu
![]()
![]() (Prvé riešenie príkladu.)
(Prvé riešenie príkladu.)
Druhá možnosť
Zavedieme pomocnú substitúciu:
![]()
![]()

Vrátime sa k substitúcií a upravíme rovnicu
![]()
![]() (Druhé riešenie príkladu.)
(Druhé riešenie príkladu.)
Výsledné riešenie zapíšeme v tvare
Príklad 3
Riešte goniometrickú rovnicu s neznámou ![]() :
:
![]()
Riešenie
![]() (Použili sme vzorce pre
(Použili sme vzorce pre ![]() .)
.)
![]() (Použili sme tabuľkové hodnoty funkcie (sínus a kosínus).)
(Použili sme tabuľkové hodnoty funkcie (sínus a kosínus).)
![]()
![]()
![]()
![]()
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
![]()
Riešime teda rovnice:
![]()
![]()

Z grafu oboch funkcií sínus a kosínus plynie:
Výsledné riešenie zapíšeme v tvare
Pre návrat na začiatok stlač => hore
Úlohy
Riešte rovnice s neznámou ![]() :
:
a)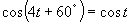
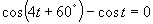
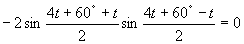 (Používame vzorce pre súčet a rozdiel goniometrických funkcií, súčtove vzorce.)
(Používame vzorce pre súčet a rozdiel goniometrických funkcií, súčtove vzorce.)
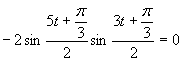 (Využijeme
(Využijeme ![]() .)
.)
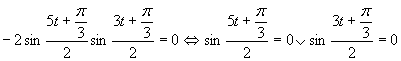 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Prvá možnosť
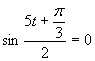 Zavedieme substitúciu
Zavedieme substitúciu 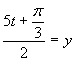 a získame rovnicu:
a získame rovnicu:
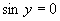

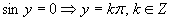 Vrátime sa k substitúcií a upravíme rovnicu
Vrátime sa k substitúcií a upravíme rovnicu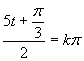
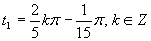
Druhá možnosť
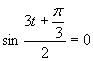 Zavedieme substitúciu:
Zavedieme substitúciu: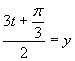
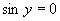

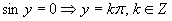 Vrátime sa k substitúcií a upravíme rovnicu
Vrátime sa k substitúcií a upravíme rovnicu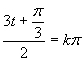
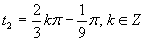
Výsledné riešenie zapíšeme v tvare
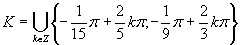 .
.
b)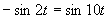
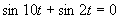
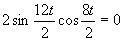 (používame vzorce uvedené v časti)
(používame vzorce uvedené v časti)
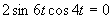
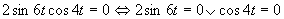 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Prvá možnosť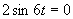
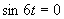 Zavedieme substitúciu:
Zavedieme substitúciu: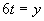
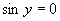

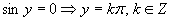 Vrátime sa k substitúcií a upravíme rovnicu
Vrátime sa k substitúcií a upravíme rovnicu 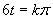 .
.
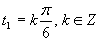
Druhá možnosť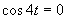 Zavedieme substitúciu:
Zavedieme substitúciu: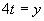
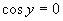

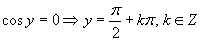 Vrátime sa k substitúcií a upravíme rovnicu
Vrátime sa k substitúcií a upravíme rovnicu 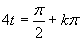 .
.
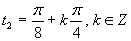
Výsledné riešenie zapíšeme v tvare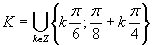 .
.
c)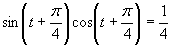
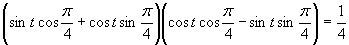 (používame vzorce uvedené v časti)
(používame vzorce uvedené v časti)
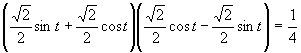 (použijeme tabuľkové hodnoty uvedené v časti)
(použijeme tabuľkové hodnoty uvedené v časti)
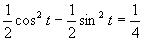
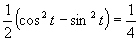
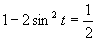
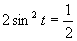
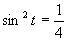
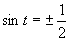

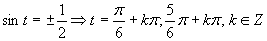 Výsledné riešenie zapíšeme v tvare
Výsledné riešenie zapíšeme v tvare 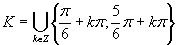 .
d)
.
d)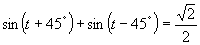
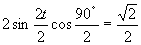 (používame vzorce uvedené v časti)
(používame vzorce uvedené v časti)
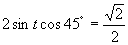 (používame tabuľkové hodnoty uvedené v časti)
(používame tabuľkové hodnoty uvedené v časti)
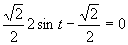
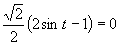 Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
Využijeme vlastnosť, kedy sa súčin rovná nule (aspoň, keď jeden činiteľ je rovný nule).
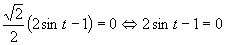
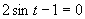
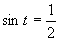

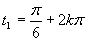 (prvé riešenie, využívame vlastnosť, že funkcia sínus je periodická)
(prvé riešenie, využívame vlastnosť, že funkcia sínus je periodická)
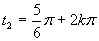 (druhé riešenie)
Výsledné riešenie zapíšeme v tvare
(druhé riešenie)
Výsledné riešenie zapíšeme v tvare 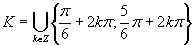 .
e)
.
e)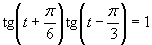
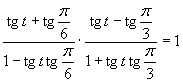 (používame vzorce uvedené v časti)
(používame vzorce uvedené v časti)
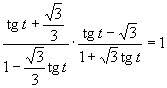 (používame tabuľkové hodnoty funkcie tangens uvedené v časti)
(používame tabuľkové hodnoty funkcie tangens uvedené v časti)
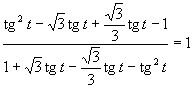
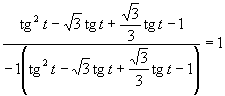
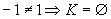 (Množina koreňov je prázdna.)
(Množina koreňov je prázdna.)
Pre návrat na začiatok stlač => hore