Goniometrické nerovnice
V tejto časti sa budeme zaoberať riešením goniometrických nerovníc. Príklady sú opäť obohatené vzorovým riešenim a úlohy určene k precvičovaniu sú doprevadzané riešením po krokoch zobrazujúcich sa po kliknutí na príklad.
Pri riešení goniometrických nerovníc využívame znalosti získane z riešenia goniometrických rovníc, riešenie je často viditeľné priamo z grafu daných funkcií alebo z jednotkovej kružnice, taktiež využívame základné tabuľkové hodnoty goniometrických funkcií.
Poznámka: Bližšie informácie o jednotkovej kružnici môžme nájsť v diplomovej práci Goniometrie a trigonometrie.
Základné goniometrické nerovnice
Riešenie základných goniometrických nerovníc je viditeľné priamo z grafov goniometrických funkcií, ako si to môžme pozrieť na úvodných vzorovo riešených príkladoch. Kapitola obsahuje aj úlohy určené k precvičovaniu, ktoré sú obohatené krokovaným riešenim. Pri riešeni základných goniometrických nerovníc sa predpokladá znalosť riešenia goniometrických rovníc, lineárnych a kvadratických nerovníc.
Príklad 1
Riešte goniometrickú nerovnicu s neznámou 
:
Riešenie
Na tomto príklade si ukážeme dve rôzne metody ako riešiť goniometrickú nerovnicu.
Prvá metóda:
V prvom prípade riešenie určíme pomocou jednotkovej kružnice.
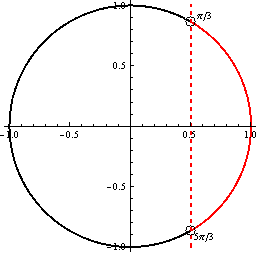
Z jednotkovej kružnice je vidieť, že daná goniometrická nerovnica nadobúda riešenie v prvom a v štvrtom kvadrante. Časť jednotkovej kružnice znázornená červenou farbou určuje riešenie danej goniometrickej nerovnice
Výsledné riešenie môžme zapísať v tvare 
, využívame podobne ako pri goniometrických rovniciach periodičnosť funkcie kosínus, platí 
.
Druhá metóda:
V druhom prípade riešenie určíme pomocou grafu funkcie kosínus.
Časť grafu znázornená červenou farbou odpovedá riešeniu danej goniometrickej nerovnice. Využitim periodičnosti funkcie kosínus dostávame výsledné riešenie, ktoré zapíšeme v tvare
.
Príklad 2
Riešte goniometrickú nerovnicu s neznámou :
Riešenie
Aby výrazy v nerovnici boli definované, musí platiť podmienka 
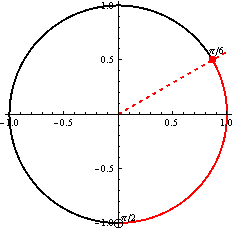
Z jednotkovej kružnice je vidieť, že riešenim je množina 
, pričom platí, že v bode 
funkcia tangens nie je definovaná, preto použijeme okrúhlu zátvorku, naopak bod 
patrí do riešenia, plynie zo zadania, preto použijeme uhlovú zátvorku.
Príklad 3
Riešte goniometrickú nerovnicu s neznámou :
Riešenie
Aby výrazy v nerovnici boli definované, musí platiť podmienka 
.
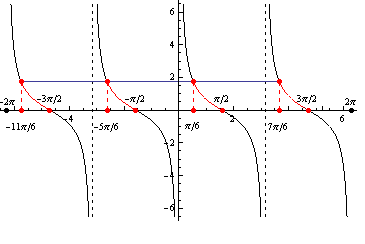
Využitím grafu a periodičnosti funkcie kotangens dostávame výsledok, ktorý zapíšeme v tvare 
.
Pre návrat na začiatok stlač => hore
Úlohy
Riešte nerovnice s neznámou 
:
a)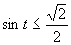
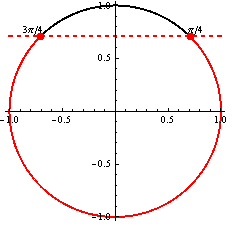Využitím jednotkovej kružnice dostávame riešenie, ktoré zapíšeme v tvare 
.
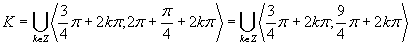b)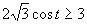
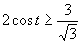
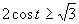
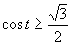
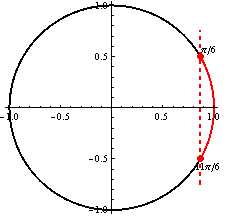Využitím jednotkovej kružnice dostávame riešenie, ktoré zapíšeme v tvare 
.
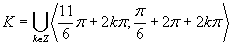c)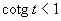
Aby výrazy v nerovnici boli definované, musí platiť podmienka: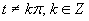 
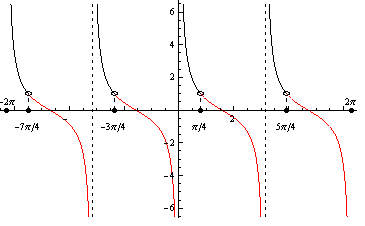Využitím grafu a periodicity funkcie kotangens dostávame výsledné riešenie, ktoré zapíšeme v tvare 
.
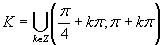d)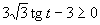
Aby výrazy v nerovnici boli definované, musí platiť podmienka: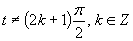 
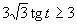
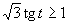
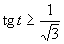
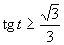
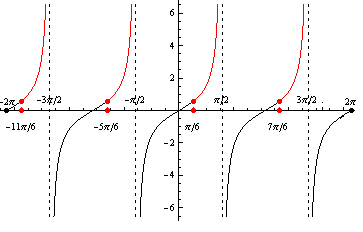Využitím grafu a periodicity funkcie tangens dostávame výsledné riešenie, ktoré zapíšeme v tvare 
.
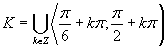e)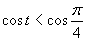
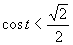(Použili sme tabuľkové hodnoty funkcie kosínus.)
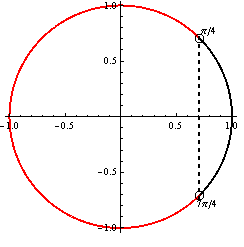Využitím jednotkovej kružnice a periodicity funkcie kosínus dostávame výsledné riešenie, ktoré zapíšeme v tvare 
.
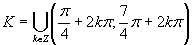Pre návrat na začiatok stlač => hore
Zložitejšie goniometrické nerovnice
Pri riešeni zložitejších goniometrických nerovníc využívame znalosti, ktoré sme získali pri riešení goniometrických rovníc a základných goniometrických nerovníc. Postupnou úpravou prevedieme zložitejšiu goniometrickú nerovnicu na základný typ goniometrických nerovníc. Kapitola obsahuje vzorové vyriešene príklady a taktiež aj úlohy určené k precvičovaniu, ktoré sú obohatené riešenim.
Príklad 1
Riešte goniometrickú nerovnicu s neznámou :
Riešenie
Zavedieme pomocnú substitúciu 
:
Situáciu zobrazíme na jednotkovej kružnici:
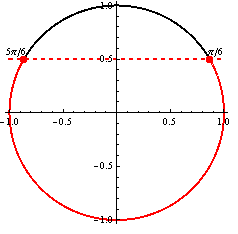
Využitím jednotkovej kružnice dostávame riešenie 
Vrátime sa k subtitúcií 
, odkiaľ plynie, že 
.
Úpravou dostávame 
.
Výsledné riešenie zapíšeme v tvare 
.
Príklad 2
Riešte goniometrickú nerovnicu s neznámou :
Riešenie
Aby výrazy v nerovnici boli definované, musí platiť podmienka: 
(Použili sme tabuľkovú hodnotu uvedenú v funkcie tangens.)
Z definície absolútnej hodnoty vyplýva:
(Bližšie informácie o absolútnej hodnote môžme nájsť v diplomovej práci Základné poznatky z matematiky na strednej škole.)
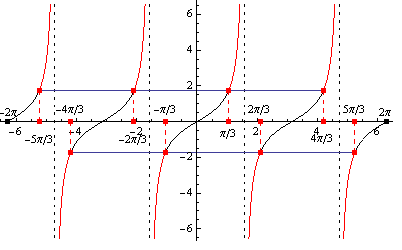
Využitím grafu funkcie a periodičnosti funkcie tangens dostávame riešenie: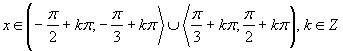 
Výsledné riešenie zapíšeme v tvare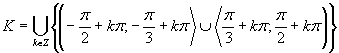
.
Príklad 3
Riešte goniometrickú nerovnicu s neznámou :
Riešenie
Využijeme graf funkcie sínus a kosínus:
Časť grafu vyznačená červenou farbou zahŕňa riešenie danej nerovnice. Je vidieť, že riešenim pri využití periódy 
je množina 
.
Príklad 4
Riešte goniometrickú nerovnicu s neznámou 
:
Riešenie
(Použili sme vzorec 
.)
(Použili sme vzorec 
.)
(Využijeme vlastnosť, kedy je súčin dvoch čísel menší ako nula).
Riešenie sa nám rozdelí na dva prípady.
Prvá možnosť
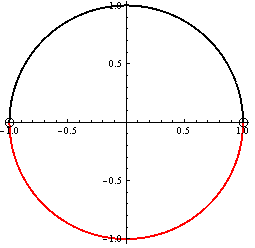
Z jednotkovej kružnice plynie, že 
.
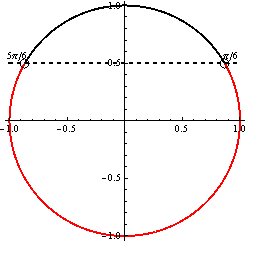
Z jednotkovej kružnice plynie, že 
.
Druhá možnosť
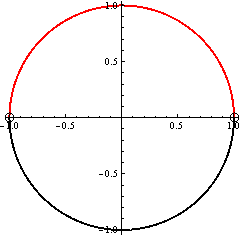
Z jednotkovej kružnice plynie, že 
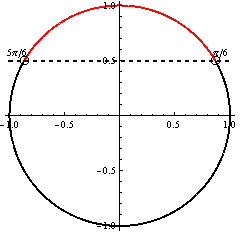
Z jednotkovej kružnice plynie, že 
(Celkově riešenie je zjednotením dvoch čiastkových.)
Výsledné riešenie zapíšeme v tvare 
.
Príklad 5
Riešte goniometrickú nerovnicu s neznámou :
Riešenie
(Použili sme vzorec .)
Zavedieme substitúciu 
.
(Určíme diskriminant a korene odpovedajúcej kvadratickej rovnice.)
Nájdené korene využíjeme k tomu, aby sme kvadratický trojčlen v nerovnici rozložili na súčin.
(Vrátime sa k substitúcií .)
(Využijeme vlastnosť, kedy je súčin dvoch čísel väčší ako nula.)
Riešenie sa nám rozdelí na dva prípady.
Prvá možnosť
, odkiaľ plynie, že 
Situáciu si znázornime na jednotkovej kružnici.
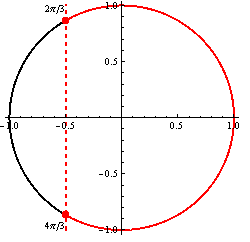
Využitím jednotkovej kružnice, periodičnosti funkcie kosínus, platí 
, dostávame riešenie, ktoré zapíšeme v tvare
.
Druhá možnosť
Odkiaľ plynie, že množina koreňov je prázdna, čo matematický zapíšeme ako 
.
(Celkově riešenie je zjednotením dvoch čiastkových.)
Výsledné riešenie zapíšeme v tvare 
.
Pre návrat na začiatok stlač => hore
Úlohy
Riešte nerovnice s neznámou :
a)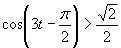
Zavedieme substitúciu 
.
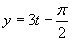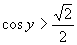
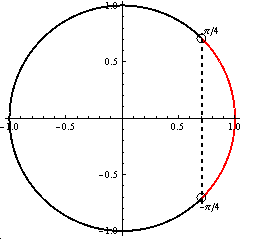Z jednotkovej kružnice je vidieť, že riešenim je 
.
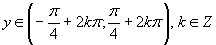Vrátime sa k substitúcií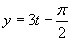 
.
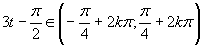
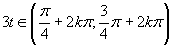
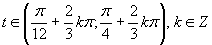Výsledné riešenie zapíšeme v tvare 
.
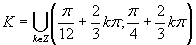b)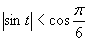
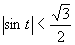(Použili sme tabuľkovú hodnotu funkcie kosínus uvedenú v časti.)
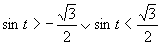(Riešenie určíme pomocou jednotkovej kružnice, pričom využívame periodičnosť.)
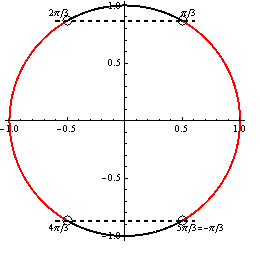Časť grafu vyznačená červenou farbou znázorňuje riešenie. Výsledné riešenie zapíšeme v tvare 
.
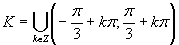c)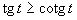
Aby výrazy v nerovnici boli definované, musia platiť podmienky: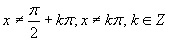 
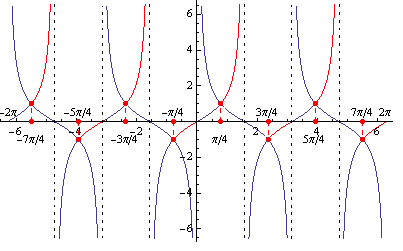Časť grafu vyznačená červenou farbou znázorňuje riešenie. Využitím periodičnosti dostávame riešenie, ktoré zapíšeme v tvare 
.
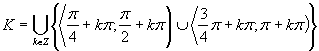d)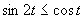
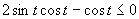(Používame vzorce uvedené v časti.)
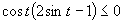(Využijeme vlastnosť, kedy je súčin dvoch čísel menší, rovný ako nula).
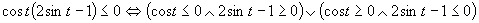
Prvá možnosť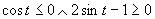 
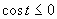
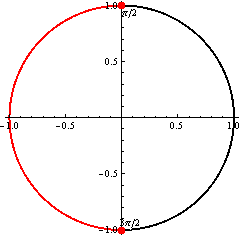
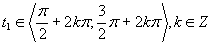
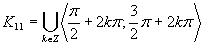
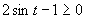
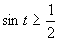
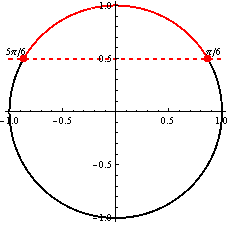
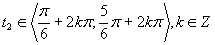
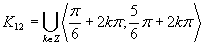
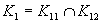
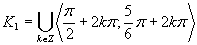(Riešenie prvej možnosti.)
Druhá možnosť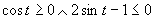 
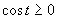
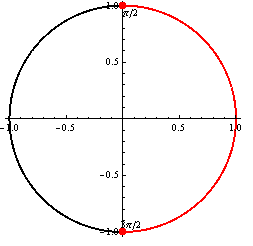
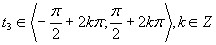
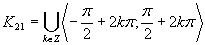
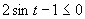
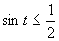
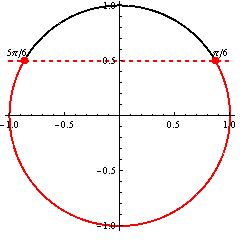
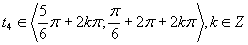
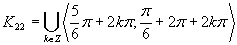
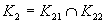
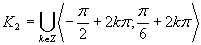(Riešenie druhej možnosti.)
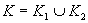(Celkové riešenie je zjednotením obidvoch rozobratých možnosti.)
Výsledné riešenie zapíšeme v tvare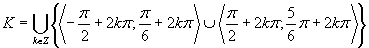 
.
e)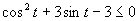
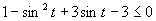(Používame vzorce uvedené v časti.)
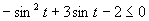
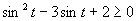Zavedieme substitúciu 
.
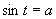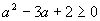(Určíme diskriminant a korene odpovedajúcej kvadratickej rovnice.)
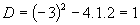
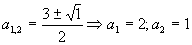(Nájdené korene využíjeme k tomu, aby sme kvadratický trojčlen v nerovnici rozložili na súčin.)
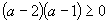Vrátime sa k substitúcií a dostávame, že 
.
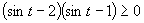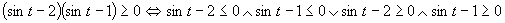
Prvá možnosť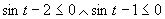 
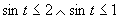
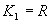(Plynie z vlastnosti funkcie sínus.)
Druhá možnosť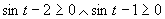 
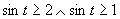
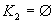(Plynie z oboru funkčných hodnôt funkcie sínus.)
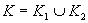(Celkové riešenie je zjednotením obidvoch rozobratých možnosti.)
Výsledné riešenie zapíšeme v tvare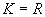 
.
Pre návrat na začiatok stlač => hore