Vzájemná poloha dvou přímek

Ve stereometrii rozlišujeme čtyři vzájemné polohy dvou přímek v prostoru.

Vzájemné polohy dvou přímek budeme ilustrovat na krychli. Můžeme rozlišit, vzhledem ke společným bodům, čtyři vzájemné polohy.

V prvních dvou případech přímky nemají žádný společný bod. Na obr. 1 jsou přímky rovnoběžné a na obr. 2 mimoběžné. V obou případech přímky nemají žádné společné body, rozdíl je v tom, jestli můžeme přímkami proložit rovinu. Rovnoběžky leží v jedné rovině, mimoběžkami nemůžeme proložit rovinu. Ve třetím příkladě jsou přímky různoběžné, tedy mají jeden společný bod, kterému říkáme průsečík. (obr. 3). Posledním případem je totožnost obou přímek, tedy obě přímky mají všechny body společné (obr. 4).

Polohy přímek na obr. 1,obr. 2 a obr. 4 známe i z planimetrie. Tedy bylo by možné je ilustrovat i v rovině. Situace z obr. 2 může nastat v prostoru, nemůže nastat v rovině.

Vzájemná poloha	Společné body	Číslo obrázku	Značení
Rovnoběžné různé	žádné	obr. 1	p \|\| q
Mimoběžné	žádné	obr. 2	p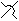q
Různoběžné	jeden	obr. 3	p q
Totožné	všechny	obr. 4	p = q

Obr. 1	Přímky jsou rovnoběžné různé, nemají žádný společný bod, leží v jedné rovině.
Obr. 2	Přímky jsou mimoběžné, nemají žádný společný bod, neleží v jedné rovině.
Obr. 3	Přímky jsou různoběžné, mají jeden společný bod, kterému říkáme průsečík. Leží v jedné rovině.
Obr. 4	Přímky jsou totožné, mají všechny body společné.

Úlohy

1. Je dána krychle ABCDEFGH. Určete vzájemné polohy daných přímek a jejich společné body, pokud existují.

AB a CD

Přímky jsou rovnoběžné různé, nemají žádný společný bod.

Skryj výsledek

Zobraz výsledek

BC a FG

Přímky jsou rovnoběžné různé, nemají žádný společný bod.

Skryj výsledek

Zobraz výsledek

AD a FD

Přímky jsou různoběžné, jejich průsečíkem je bod D.

Skryj výsledek

Zobraz výsledek

EF a CG

Přímky jsou mimoběžné, nemají žádný společný bod.

Skryj výsledek

Zobraz výsledek

2. Je dána krychle ABCDEFGH a body L, M, N, P jsou po řadě středy hran AB, BF, EF, CD. Rozhodněte o vzájemné poloze přímek.

DM a NP

Přímky jsou mimoběžné.

Skryj výsledek

Zobraz výsledek

DL a GM

Přímky jsou různoběžné.

Skryj výsledek

Zobraz výsledek

BN a CF

Přímky jsou mimoběžné, nemají žádný společný bod.

Skryj výsledek

Zobraz výsledek

3. Je dán pravidelný čtyřboký jehlan ABCDV a body L,M,N,P jsou po řadě středy hran AB, BC, CD, DV. Rozhodněte o vzájemné poloze přímek.

LM a DC

Přímky jsou různoběžné.

Skryj výsledek

Zobraz výsledek

LN a BM

Přímky jsou rovnoběžné.

Skryj výsledek

Zobraz výsledek

MN a AV

Přímky jsou mimoběžné, nemají žádný společný bod.

Skryj výsledek

Zobraz výsledek

4. Je dán čtyřstěn ABCV a body L,M,N,P jsou po řadě středy hran AB, BC, AV, BV. Rozhodněte o vzájemné poloze přímek.

AB a PV

Přímky jsou různoběžné. Vrchol B je průsečík.

Skryj výsledek

Zobraz výsledek

BM a AV

Přímky jsou mimoběžné, nemají žádný společný bod.

Skryj výsledek

Zobraz výsledek

CV a BL

Přímky jsou mimoběžné, nemají žádný společný bod.

Skryj výsledek

Zobraz výsledek

5. Máme dánu krychli ABCDEFGH. Určete pomocí vrcholů krychle všechny přímky, které jsou mimoběžné s přímkou CD a leží v rovině přední stěny ABEF.

Jsou to přímky AE, BF, BE a AF.

Skryj výsledek

Zobraz výsledek

6. Máme dánu krychli ABCDEFGH. Určete pomocí vrcholů krychle všechny přímky, které jsou různoběžné s přímkou AG a prochází vrcholem B.

Řešením jsou přímky BA, BG a BH.

Skryj výsledek

Zobraz výsledek

7. Je dán pravidelný čtyřboký jehlan ABCDV. Určete pomocí vrcholů krychle všechny přímky, které jsou mimoběžné s přímkou AC.

Jsou to přímky BV a DV.

Skryj výsledek

Zobraz výsledek

8. Je dán pravidelný čtyřstěn ABCD. Určete, které z přímek určených vrcholy čtyřstěnu jsou s přímkou BD různoběžné a které jsou mimoběžné.

S přímkou BD jsou různoběžné přímky AD, CD, AB, CB. Mimoběžná je pouze přímka AC.

Skryj výsledek

Zobraz výsledek