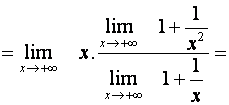Příklady

Určete .

Protože funkce y = x² je spojitá v bodě 3, můžeme přímo dosadit a určit limitu díky vztahu mezi limitou a spojitostí.

Určete .

Použijeme větu o limitě součtu a protože funkce y = x² a y = x-1 jsou spojité v bodě 2 můžeme počítat takto:

Určete .

Použijeme větu o limitě součinu a využijeme spojitosti.

 Určete .

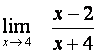Použijeme větu o limitě podílu a využijeme spojitosti.

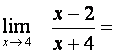
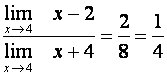
Určete .

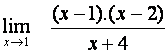Použijeme větu o limitě součinu a podílu a využijeme spojitosti.

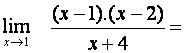
Určete .

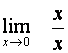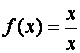Nemůžeme použít větu o limitě podílu, neboť bychom získali neurčitý výraz . Můžeme ale provést následující úpravu: . Máme tedy funkci  s definičním oborem D_f = R \ {0} a  s definičním oborem D_g = R. Funkce g je spojitá v 0 a navíc jsou splněny předpoklady věty o dvou funkcích( f(x) = g(x) na R \ {0}), takže platí:

Určete .

Pro x jdoucí k +¥ se funkční hodnoty také blíží k +¥. Je tedy

Určete .

Úvahu z předchozího příkladu nemůžeme použít, získali bychom totiž výraz ¥−¥. Upravíme tedy výraz následujícím způsobem:

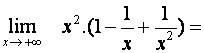
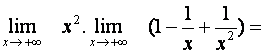
Nyní můžeme použít větu o limitě součtu a součinu a dostáváme tak:

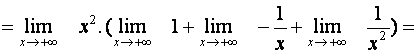
Určete .

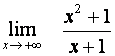Nemůžeme použít větu o limitě podílu, neboť bychom získali neurčitý výraz . Můžeme ale použít podobnou úpravu jako v předchozím příkladu.

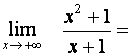
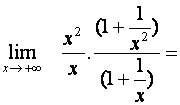
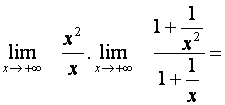
Limitu se zlomkem určíme pomocí věty o limitě součtu a podílu