Dělicí poměr
Nejdříve si zavedeme pojem dělicí poměr, který budeme dále využívat. Týká se každých tří různých bodů ležících na jedné přímce a jejich vzájemných vzdáleností.
Definice
Nechť A, B, C jsou tři libovolné různé kolineární body.
Dělicí poměr bodu C vzhledem k bodům A, B v daném pořadí je reálné číslo, jehož absolutní hodnota je rovna podílu |AC|:|BC|, a toto číslo:
- je kladné, není-li bod C bodem úsečky AB;
- je záporné, je-li bod C vnitřní bod úsečky AB.
Označení: (ABC).
Rozbor definice
V definici je dán předpoklad, že vezmeme tři různé kolineární body. Co by se stalo, kdyby nebyly různé? Rozeberme si jednotlivé případy.
- C=A, A
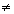B, pak |(ABC)|=0/|BC|=0 - C=B, A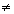B, pak (ABC) není definován, neboť |BC|=0 a nulou nelze dělit
Také je zajímavá otázka, zda dělicí poměr může nabývat hodnoty 1. Nemůže!
Mějme různé body A, B ležící na přímce, jako je na obrazku níže. Bod C zkusíme umístit na přímku tak, aby (ABC)=1. Dělicí poměr je kladný, bod C bude tedy ležet mimo úsečku AB. I když budeme bod C posouvat dále (viz šedé body na obrázku níže), dělicí poměr se bude zmenšovat, blížit k 1, ale nikdy nebude roven 1. To si také můžete vyzkoušet na apletu výše.
Z uvedeného vyplývá, že máme-li dva různé body A, B na dané přímce, pak polohy každého dalšího bodu C této přímky můžeme jednoznačně zadat dělícím poměrem (ABC).
Nyní si ukážeme příklady na dělicí poměr. V příkladech jsou použity obrázky, na kterých je znázorněna přímka a na ní příslušné body. Vzdálenost bodů snadno zjistíme z obrázku a to tak, že spočítáme úseky mezi body, které jsou oddělené puntíky; každý úsek má délku 1cm.
Příklad 1
Mějme dány body A, B, C ležící na přímce, jak je to naznačeno na obrázku níže. Určete dělicí poměr bodu C vzhledem k bodům A, B. (ABC) = ?
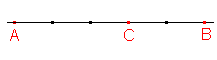
Řešení
Dělicí poměr bodu C vzhledem k bodům A, B je dán (až na znaménko) poměrem |AC|:|BC|. |AC| je vzdálenost bodů A, C a |BC| je vzdálenost bodů B, C.
|AC| = 3 cm; |BC| = 2 cm
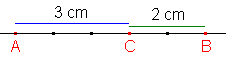
Protože bod C leží na úsečce AB, dělicí poměr bude číslo záporné.
(ABC) = -|AC|:|BC| = -3/2
Příklad 2
Určete bod D na přímce AB tak, aby (ABD) = 3/4.
Řešení
Dělicí poměr bodu D vzhledem k bodům A,B je číslo kladné, tedy bod D bude ležet vně úsečky AB a to buď takto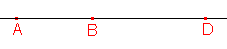 
, nebo 
.
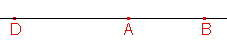Dále z dělicího poměru víme, že vzdálenost bodu D od bodu A je 3 cm a vzdálenost bodu D od bodu B je 4 cm. Bod A je tedy blíže k bodu D, jako je to na druhém obrázku. Po nanesení přesných vzdáleností získáme tento výsledek: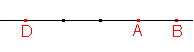 
.
Úlohy
- 1. Z obrázku zjistěte dělicí poměr:
- a) (ABC) = ?
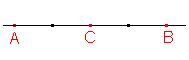
(ABC) = -|AC|:|BC| = -2:2 = -1
Skryj výsledekZobraz výsledek - b) (ABD) = ?
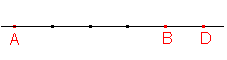
(ABD) = |AD|:|BD| = 5:1 = 5
Skryj výsledekZobraz výsledek - c) (ACD) = ?
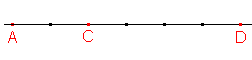
(ACD) = |AD|:|CD| = 6:4 = 3/2
Skryj výsledekZobraz výsledek
- 2. Na přímce znázorněte body A, B, C tak, aby platilo:
- a) (ACB) = -2
Řešení vypadá takto: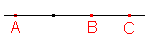
Skryj výsledekZobraz výsledek - b) (BCA) = 4/3
Řešení vypadá takto: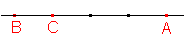
Skryj výsledekZobraz výsledek - c) (ADB) = -3/2
Řešení vypadá takto: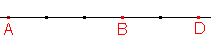
Skryj výsledekZobraz výsledek
3. Z obrázku zjistěte dělicí poměry: (ABC), (ACB), (BAC), (CAB), (CBA).
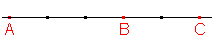
(ABC) = |AC|:|BC| = 5/2
(ACB) = -|AB|:|CB| = -3/2
(BAC) = |BC|:|AC| = 2/5
(CAB) = -|CB|:|AB| = -2/3
(CBA) = |CA|:|BA| = 5/3