Speciální posloupnosti


Různých druhů posloupností je mnoho. Na této stránce se blíže seznámíme se dvěma speciálními typy posloupností. Budou to aritmetické posloupnosti a geometrické posloupnosti .


Aritmetická posloupnost


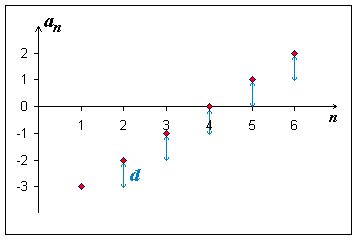
Definice: Posloupnost (an) se nazývá aritmetická právě tehdy, když

Číslo d se nazývá diference aritmetické posloupnosti.


 

... a to je právě tehdy, když každý člen posloupnosti (kromě prvního) je aritmetickým průměrem "svých sousedů".


Příklady:

{-1, 1, 3, 5, 7, ... } -------> diference   d = 2
an= -5n - 13 -------> diference   d = -5
an= an-1 + 0,1 ,  a1 = 1 -------> diference   d = 0,1

vlastnosti aritmetických posloupností

monotónnost
a) rostoucí <=> d > 0
b) klesající <=> d < 0
omezenost
a) shora omezená <=> d < 0
b) zdola omezená <=> d > 0
c) omezená <=> d = 0

Příklady:

{ -1, 1, 3, 5, 7, ... } -------> diference  d = 2
-------> rostoucí, zdola omezená
an= - 5n - 13 -------> diference  d = -5
-------> klesající, shora omezená
an= an-1 + 0,1 ,  a1 = 1 -------> diference  d = 0,1
-------> rostoucí, zdola omezená

vztahy platící pro aritmetické posloupnosti

n-týčlen aritmetické posloupnosti
an= a1 + (n - 1) d
součet prvních n členů aritmetické posloupnosti


Geometrická posloupnost


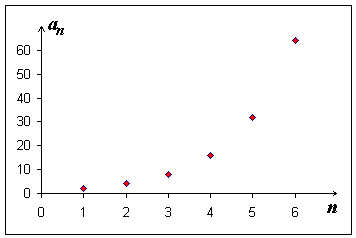
Definice: Posloupnost (an) se nazývá geometrická právě tehdy, když

Číslo q se nazývá kvocient geometrické posloupnosti.


... a to je právě tehdy, když každý člen posloupnosti (kromě prvního) je geometrickým průměrem "svých sousedů".


Příklady:

{ -1, 1, -1, 1, -1, ... } -------> kvocient   q = -1
an = 1/2n -------> kvocient   q = 1/2
an = 4an-1,   a1 = 1  -------> kvocient   q = 4

vlastnosti geometrických posloupností

monotónnost
a) rostoucí <=> a1 > 0 ,  q > 1 nebo a1 < 0 ,  0 < q < 1
b) klesající <=> a1 > 0,  0 < q < 1  nebo a1 < 0 ,  q > 1
omezenost
a) shora omezená <=>  a1 < 0,  q > 1
b) zdola omezená <=> a1 > 0,  q > 1
c) omezená <=> | q | < 1     nebo       | q | = 1      nebo      a1 = 0

Příklady:

{ -1, 1, -1, 1, -1, ... } -------> kvocient   q = -1 ,  a1 = -1
-------> ani rostoucí, ani klesající, omezená
an = 1/2n -------> kvocient   q = 1/2 ,  a1 = 1/2 
-------> klesající, omezená
an = 4 an-1 ,  a1 = 1  -------> kvocient   q = 4,  a1 = 1 
-------> rostoucí, zdola omezená

vztahy platící pro geometrické posloupnosti

n-tý člen geometrické posloupnosti

an= a1 qn - 1
součet prvních n členů geometrické posloupnosti
 sn= n an pokud   q = 1
pokud   q 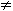1


Odkazy na cizí stránky zabývající se tímto tématem:

- test: aritmetická vs. geometrická posloupnost
- příklady: členy aritmetické posloupnosti
- součet prvních n členů aritmetické posloupnosti
- příklady: aritmetická posloupnost
- příklady: členy geometrické posloupnosti
- součet prvních n členů geometrické posloupnosti
- příklady: geometrická posloupnost
- test: vzorečky


Příklady

aritmetické posloupnosti

1. Zjistěte, zda jsou zadané posloupnosti aritmetické, a pokud ano, určete jejich první člen a diferenci.

a)
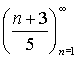
b)   

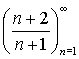
2. Určete reálné číslo x tak, aby čísla a1, a2, a3 tvořila tři následující členy aritmetické posloupnosti.

a)
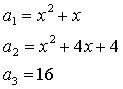
b)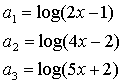  

3. V aritmetické posloupnosti je a1 = 64  a d = 4. Kolikátý člen je roven číslu 100?

4. V aritmetické posloupnosti je a1 = 5  a d = 3 určete, kolik členů této posloupnosti musíme sečíst, aby součet byl větší než  100.

5. Určete první člen a diferenci aritmetické posloupnosti, ve které platí:

a)
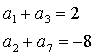
b)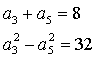  

6. Délky stran pravoúhlého trojúhelníku tvoří tři po sobě jdoucí členy aritmetické posloupnosti. Obvod tohoto trojúhelníku je 96cm. Vypočítejte délky stran.

7. Řešte rovnici a nerovnici s neznámou x N.

a)
b)  

geometrické posloupnosti

8. Zjistěte, zda jsou zadané posloupnosti geometrické, a pokud ano, určete jejich první člen a kvocient.

a)
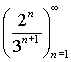
b)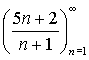

9. Určete reálné číslo x tak, aby čísla a1, a2, a3 tvořila tři následující členy geometrické posloupnosti.

 

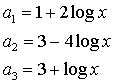10. Určete první člen a kvocient geometrické posloupnosti, ve které platí: 

a)
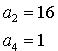
b)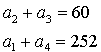  

11. V geometrické posloupnosti s prvním členem  a1= 36 určete kvocient tak, aby platilo: s3 252.

12. Řešte rovnici a nerovnici s neznámou x N.

a)
b)  

13. Za pět let se počet obyvatel ve městě X zvýšil o 12%. Jaký byl roční přírůstek obyvatel?