Řady
S pojmem posloupnost je úzce spojen pojem řada. Řada vznikne sečtením prvků posloupnosti. Pokud je posloupnost konečná, vznikne konečná řada , pokud je posloupnost nekonečná, vznikne sečtením jejích členů nekonečná řada .
Definice: Je dána posloupnost (an). Výraz tvaru
| a1 + a2 + a3 + ... + an + ... |
se nazývá řada.
Členy posloupnosti se nazývají členy řady.
Pokud je posloupnost konečná, tedy
![]() vznikne konečná řadu a zapisuje se
vznikne konečná řadu a zapisuje se
Pokud je posloupnost nekonečná, tedy
![]() vznikne nekonečná řada a zapisuje se
vznikne nekonečná řada a zapisuje se
Jelikož řada je definovaná jako součet, budeme se hlavně zajímat o to, zda danou řadu lze nebo nelze sečíst, a pokud ano, tak jaký je tento součet.
Nekonečné řady
Definice: Řada se nazývá konvergentní, pokud je její součet reálné číslo. V opačném případě se řada nazývá divergentní.
Pojem konvergence a divergence je známý již z limit. Zde se vyskytuje zcela oprávněně, protože možnost sečíst řadu opravdu souvisí s existencí limity určité posloupnosti a to posloupnosti částečných součtů.
posloupnost částečných součtů ( sn)
Máme dánu posloupnost (an). Člen posloupnosti částečných součtů sk vznikne jako součet a1 + a2 + a 3 + ... + ak. Tedy
| s1 = a1 | |
| s2 = a1 + a2 | |
| s3 = a1 + a2 + a3 | |
| ... | |
| sk = a1 + a2 + a3 + ... + ak | |
| ... |
Příklad:
Je dána posloupnost an = 1/2n = { 1/2, 1/4, 1/8, 1/16, ... }
Posloupnost částečných součtů bude vypadat následovně:
|
|
s1 = a1 = 1/2 = 0,5 | |
|
|
||
|
|
s2 = a1 + a2 = 1/2 + 1/4 = 0,75 | |
|
|
||
|
|
s3 = a1 + a2 + a3 = 1/2 + 1/4 + 1/8 = 0,875 | |
|
|
||
|
|
s4 = a1 + a2 + a3 + a4 = 1/2 + 1/4 + 1/8 + 1/16 = 0,9375 | |
|
|
||
|
|
s5 = a1 + a2 + a3 + a4 + a5 = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 = 0,96875 | |
|
|
||
| ... |
Z tohoto příkladu by už mohlo být vidět, jak souvisí součet řady s posloupností částečných součtů. Je vidět, že členy této posloupnosti se se vzrůstajícím n stále více blíží k 1. Můžeme se tedy domnívat, že pokud součet "všech" členů posloupnosti (an), tedy součet řady bude právě 1.
součet nekonečné řady
Věta1: Řada je konvergentní právě tehdy, když je konvergentní posloupnost částečných součtů a limita posloupnosti částečných součtů je rovna součtu této řady.
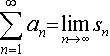 |
|
Příklad:
Vezmeme posloupnost z minulého příkladu, tady an = 1/2n = { 1/2, 1/4, 1/8, 1/16, ... }
Tato posloupnost je geometrická (a1 = 1/2, q = 1/2), podle vzorce umíme tedy sečíst vždy prvních k členů:
Posloupnost částečných součtů bude vypadat následovně:
| s1= 1/2 = 1/2 | ||
| s2= 1/2 + 1/4 = 3/4 | ||
| ... |
|
|
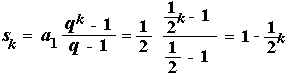
|
||
| ... | ||
... součet řady bude tedy vypadat následovně ...
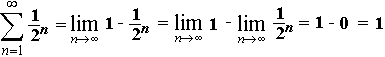 |
Tato řada konverguje, protože konverguje posloupnost částečných součtů.
Příklad:
Nyní zkusíme, jak bude vypadat řada vznikla z posloupnosti an = n = { 1, 2, 3, 4, ... }
Tato posloupnost je aritmetická (a1 = 1, d = 1), podle vzorce umíme tedy sečíst vždy prvních k členů:
Posloupnost částečných součtů bude vypadat následovně:
| s1 = 1 = 1 | |||
| s2 = 1 + 2 = 3 | |||
| ... |
|
||
|
|
|||
| ... | |||
... součet řady bude tedy vypadat následovně ...
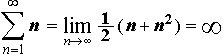 |
Tato řada je divergentní, protože diverguje posloupnost částečných součtů.
nekonečná geometrická řada
Speciálním typem nekonečné řady je nekonečná geometrická řada. Ta vznikne z geometrické posloupnosti. Tato řada má tu příjemnou vlastnost, že existuje jednoduché kriterium konvergence a pokud je řada konvergentní, lze pomocí vzorce vyjádřit její součet.
Máme nekonečnou geometrickou řadu s prvním členem a1 a kvocientem q, potom ...
| |q| < 1 | ---------> | řada konverguje | |
|
|q|
|
---------> | řada diverguje |
Pokud řada konverguje, potom platí
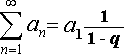 |
|
Konečné řady
U konečných řad nemá smysl se bavit o tom, zda řadu jde nebo nejde sečíst. Konečně mnoho čísel jde vždy sečíst (přinejhorším hrubou silou).
|
|
Tato metoda ale není nejvhodnější, pokud má řada víc členů (sečtěte prvních 10 625 členů posloupnosti ...). Pro takové případy lze odvodit vzorce na součet několika základních konečných řad.
|
|
||
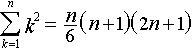
|
|
|
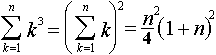
|
Odkazy na cizí stránky zabývající se tímto tématem:
|
|
- počítá součet konečné řady |
|
|
|
- počítá součet konečné řady - vypíše posloupnost částečných součtů |
|
|
|
- příklady: zápis pomocí sumy | |
|
|
- příklady: zápis pomocí sumy |
konečné řady
1. Zapište pomocí sumy:
| a) | 5 + 7 + 9 + 11 + ... + 27 |
|
|
| b) | -1 + 2 - 4 + 8 - 16 + ... -1024 |
|
2. Vypočítejte:
| a) |
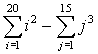
|
|
|
| b) | 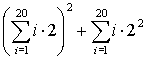 |
|
nekonečné geometrické řady
3. U daných nekonečných geometrických řad určete první člen a kvocient. Rozhodněte, zda je daná řada konvergentní a pokud ano, určete její součet.
| a) |
|
|
|
| b) | 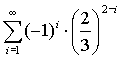 |
|
4. Určete, pro která reálná x jsou dané řady konvergentní a určete jejich součet.
| a) |
|
|
|
| b) | 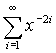 |
|
5. Řešte rovnice s neznámou x.
| a) |
|
|
|
| b) | 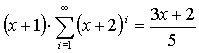
|
|
6. Slovní úlohy: