Řady - příklady
konečné řady
|
1. Zapište pomocí sumy: |
Řešení:
Postup je alespoň na začátku podobný, jako u určování vzorce pro n-tý člen posloupnosti zadané výčtem hodnot.
| 5 + 7 + 9 + 11 + ... + 27 = |
|
|
|
|
| -1 + 2 - 4 + 8 - 16 + ... -1024 = |
|
|
|
|
|
2. Vypočítejte: |
Řešení:
K řešení těchto příkladů je vhodné použít některý ze vzorců pro součet konečných řad.
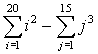
|
|
|
|
|
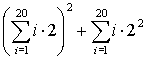
|
|
|
|
|
nekonečné geometrické řady
|
3. U daných nekonečných geometrických řad určete první člen a kvocient. Rozhodněte, zda je daná řada konvergentní a pokud ano, určete její součet. |
Řešení:
Nekonečná geometrická řada je konvergentní právě tehdy, když pro její kvocient q platí: |q| < 1.
|
|
|
|
|
|
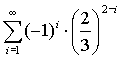
|
|
|
|
|
|
4. Určete, pro která reálná x jsou dané řady konvergentní a určete jejich součet. |
Řešení:
Nekonečná geometrická řada je konvergentní právě tehdy, když pro její kvocient q platí: |q| < 1.
|
|
|
|
|
|
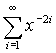
|
|
|
|
|
|
5. Řešte rovnice s neznámou x. |
Řešení:
Nekonečná geometrická řada je konvergentní právě tehdy, když pro její kvocient q platí: |q| < 1.
|
|
|
|
|
|
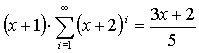
|
|
|
|
|
|
6. Slovní úlohy: |
Řešení:
Tyto slovní úlohy vedou na hledání součtu nekonečné geometrické řady.
| "Nekonečná" spirála se skládá z polokružnic, poloměr první polokružnice je 6cm, poloměr každé další polokružnice je o 1/3 menší než poloměr kružnice předcházející. Vypočítejte délku spirály. |
|
|
|
|
|
Vypočítejte délku "nekonečné" lomené čáry, která se skládá z úseček B1B2, B2B3, B3B4, B4B5, ... . Souřadnice krajních bodů úseček jsou:
|
|
|
|
|