Limita posloupnosti
Vlastní limita posloupnosti
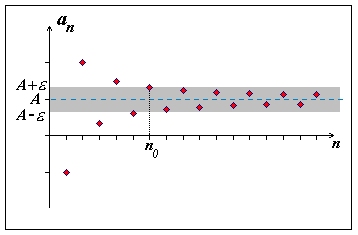
Definice: Reálné číslo A se nazývá vlastní limita posloupnosti (an) právě tehdy, když
... a značí se
|
|
(Limita posloupnosti se vždy určuje v nevlastním bodě, můžeme si tedy dovolit dále psát pouze lim an = A.)
|
|
Posloupnost se nazývá konvergentní, pokud má vlastní (reálnou) limitu A.
Posloupnost se nazývá divergentní, pokud není konvergentní.
Věty o limitách posloupností
Věta1: Každá posloupnost má nejvýše jednu limitu.
|
|
Věta2: Každá konvergentní posloupnost je omezená.
|
|
|
Věta3: Každá omezená monotónní posloupnost je konvergentní.
Každá shora omezená neklesající posloupnost je konvergentní.
Každá zdola omezená nerostoucí posloupnost je konvergentní.
Věta4:
| , kde r > 0 |
|
|
Věta5: Nechť (an) a (bn) jsou konvergentní posloupnosti a
nechť lim an = A a lim bn = B,
nechť c libovolné reálné číslo.
Potom jsou konvergentní i posloupnosti (an+ bn), (an- bn), (an.bn), (c.an) a platí
| lim (an+ bn) = lim an + lim bn = A + B | |
| lim (an- bn) = lim an- lim bn = A - B | |
| lim (an. bn) = lim an. lim bn = A . B | |
| lim (c.an) = c . lim an = c . A |
|
|
Nechť navíc jsou nenulová čísla B a bn pro všechna přirozená n.
Potom je konvergentní i posloupnost (an/bn) a platí
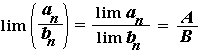 |
Nevlastní limita posloupnosti
Definice: Řekneme, že posloupnost (an) má nevlastní limitu pokud buď
... a značí se
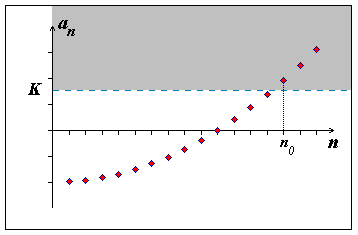
|
|
..., a nebo
... a značí se
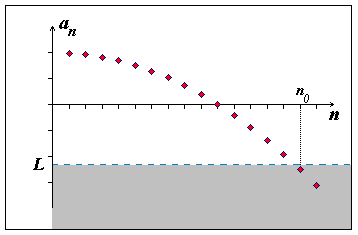
|
|
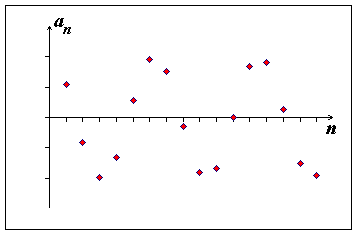
Pro každou posloupnost nastane právě jedna z následujících možností:
1. posloupnost má vlastní (reálnou) limitu
 |
2. posloupnost má nevlastní limitu
 |
 |
3. limita posloupnosti neexistuje
 |
Limity speciálních posloupností
Aritmetická posloupnost
Nechť (an) je aritmetická posloupnost s diferencí d, potom ...
| d = 0 | ---------> | konvergentní |
|
|
|
|
---------> | divergentní |
|
Geometrická posloupnost
Nechť (an) je geometrická posloupnost s kvocientem q, potom ...
|
|
---------> | divergentní | ||
| |q| < 1 | ---------> | konvergentní | ||
| lim an= 0 |
|
|||
| q = 1 | ---------> | konvergentní | ||
| q > 1 | ---------> | divergentní |
Odkazy na cizí stránky zabývající se tímto tématem:
|
|
- počítání limit (funkce) |
|
|
|
- test: konvergentní vs. divergentní posloupnost |
limita posloupnosti
1. Určete následující limity posloupností:
| a) |
|
|
|
| b) | 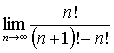 |
|
|
| c) |
|
||
| d) | 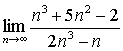 |
|
|
| e) | 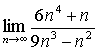 |
|
|
| f) |
|
||
| g) | 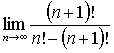 |
|
|
| h) |
|
||
| ch) | 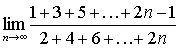 |
|