Variace, permutace, kombinace
Permutace
Permutace je zvláštní případ variace, kde k = n. To znamená, že ze zadaných prvků postupně vybereme všechny. Každá permutace tedy odpovídá nějakému pořadí zadaných prvků: každý prvek se v pořadí musí objevit, ale žádný tam nemůže být dvakrát.
Permutace z n prvků je každá n-členná variace z těchto prvků.
Permutace z n prvků je uspořádaná n-tice sestavená
z těchto prvků tak,
že každý se v ní vyskytuje právě jednou.
Počet permutací z n prvků odvodíme ze vzorce pro počet n-členných
variací z n prvků:
V(k, n) = n ·
(n − 1) · (n − 2) ·
… · (n − k + 1)
Pro k = n:
V(n, n) = n ·
(n − 1) · (n − 2) ·
… · (n − n + 1) =
= n · (n − 1) · (n − 2) ·
… · 1.
Počet P(n) všech permutací z n prvků je
P(n) = n · (n − 1) ·
(n − 2) · … · 3 · 2 · 1.
Příklad
Určete počet všech permutací prvků a, b, c.
Řešení
Počet prvků je 3, proto počítáme P(3):
P(3) = 3 · 2 · 1 = 6.
Odpověď: Počet všech permutací prvků a, b, c je 6.
Pro kontrolu je můžeme vyjmenovat:
(a, b, c),
(a, c, b),
(b, a, c),
(b, c, a),
(c, a, b),
(c, b, a).
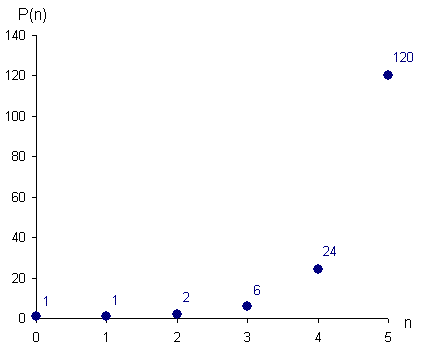
Počet permutací narůstá velmi rychle, pro větší hodnoty n bychom je už vyjmenovávali těžko. Pro ilustraci je zde tabulka prvních několika hodnot P(n) a graf.
| P(0) | 1 |
| P(1) | 1 |
| P(2) | 2 |
| P(3) | 6 |
| P(4) | 24 |
| P(5) | 120 |
| P(6) | 720 |
| P(7) | 5 040 |
| P(8) | 40 320 |
| P(9) | 362 880 |
| P(10) | 3 628 800 |
| ... | ... |
| P(20) | 2 432 902 008 176 640 000 |
Pro přirozená čísla n ≤ 170 můžete pro výpočet P(n) využít následující skript:
| n = | ||
| P(n) = | ||
Faktoriál
Pro každé přirozené číslo n definujeme:
n! = 1 · 2 · 3 · …
· (n − 1) · n
(Symbol n! čteme "n faktoriál".)
Počet P(n) všech permutací z n prvků můžeme pomocí faktoriálu zapsat takto:
Jak a proč definovat 0! ?
0! = 1
Počet V(k, n) všech k-členných variací z n prvků je
| V(k, n) = n · (n − 1) · (n − 2) · … · (n − k + 1) = |
| = | n · (n − 1) · (n − 2)
· … · (n − k + 1) ·
|
= |
| = | n! (n − k)! |
Když do vzorce dosadíme k = n, dostaneme výraz:
| V(n, n) = | n! (n − n)! |
= | n! 0! |
Z první definice permutace víme, že V(n, n) = P(n) = n!. Aby platila rovnost n! / 0! = n!, definuje se 0! = 1.
Pro přirozená čísla n, k; k ≤ n platí
| V(k, n) = | n! (n − k)! |
Příklad
Zjednodušte výraz:
(n + 1)!
n! |
− | (2n)!
(2n + 1)! |
+ | (3n − 1)!
(3n − 2)! |
Řešení
(n + 1)!
n! |
− | (2n)!
(2n + 1)! |
+ | (3n − 1)!
(3n − 2)! |
= |
| = | (n + 1) · n!
n! |
− | (2n)!
(2n + 1) · (2n)! |
+ | (3n − 1) · (3n − 2)!
(3n − 2)! |
= |
| = | (n + 1) | − | 1
2n + 1 |
+ | (3n − 1) | = |
| = | (n + 1) · (2n + 1) − 1 + (3n − 1) · (2n + 1)
2n + 1 |
= |
| = | 8n2 + 4n − 1
2n + 1 |
Výraz má smysl pro n z množiny přirozených čísel.
Pro n = 0 nejsou definované
výrazy
(3n − 1)! a (3n − 2)!.
Příklad
Určete, kolika způsoby může 10 táborníků při nástupu na ranní rozcvičku nastoupit
a) do řady;
b) do řady, v níž je táborník Aleš na kraji;
c) do řady, v níž táborníci Aleš a Zdeněk nestojí vedle sebe.
Řešení
a) Jde o počet permutací z 10 prvků, takže počet způsobů, jak 10 táborníků může nastoupit do řady, je P(10) = 10!.
b) Nejprve postavíme Aleše stranou a necháme nastoupit ostatních 9 táborníků. Podobně jako v případě a) jde o počet permutací z 9 prvků, počet způsobů seřazení je tedy P(9) = 9!. Aleš se potom může zařadit buď na levý nebo na pravý kraj. Celkem je tedy 2 · 9! způsobů seřazení 10 táborníků tak, aby byl Aleš na kraji.
c) Nejprve si uvědomíme, že platí následující rovnost:
počet všech seřazení = (počet takových seřazení, že Aleš a Zdeněk stojí vedle sebe)
+ (počet takových seřazení, že Aleš a Zdeněk vedle sebe nestojí).
Počet všech seřazení jsme vypočítali v případě a), víme tedy, že jejich počet je 10!.
Počet způsobů, jak seřadit 10 táborníků tak, aby Aleš a Zdeněk stáli vedle sebe,
určíme snadno: spojíme je do dvojice a počítáme, kolika způsoby lze
seřadit 9 prvků (8 táborníků + 1 dvojice). To lze 9! způsoby. Musíme si sle uvědomit,
že Aleš a Zdeněk mohou být ve dvojici dvěma způsoby (Aleš vlevo a Zdeněk vpravo, nebo naopak).
Celkem je tedy počet způsobů, jak seřadit 8 táborníků a jednu dvojici, 2 · 9!.
Teď už snadno zjistíme, kolik je způsobů seřazení deseti táborníků tak, aby Aleš a Zdeněk vedle
sebe nestáli: stačí od počtu všech možných seřazení odečít počet takových, kde Aleš a Zdeněk
stojí vedle sebe:
10! − 2 · 9! = 10 · 9! − 2 · 9! = 8 · 9!.