Vlastnosti posloupností


Jelikož posloupnosti jsou pouze speciální typ funkce, vlastnosti a jejich definice vám jistě budou povědomé. U posloupností se ale většinou zkoumá pouze monotónnost a omezenost dané posloupnosti. Tím lépe, nebude toho tolik.

Monotónnost posloupnosti


1. rostoucí posloupnost

Definice: Posloupnost (an) se nazývá rostoucí právě tehdy, když

Pro zjišťování, zda je posloupnost rostoucí se nám bude více hodit následující věta. Bude řečena pouze pro nekonečnou posloupnost s definičním oborem N, po drobné úpravě by ovšem platila i pro konečné posloupnosti. U konečných posloupností je třeba dát pozor na "kraje" definičního oboru.

Věta: Posloupnost je rostoucí právě tehdy, když



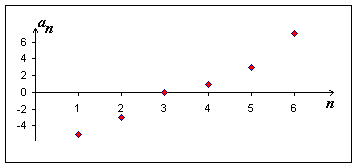Příklady:

{ -1, 1, 3, 5, 7, ... }
an = 5n2 - 13
an = an-1 + 5 ,  a1 = 1

2. klesající posloupnost

Definice: Posloupnost (an) se nazývá klesající právě tehdy, když

 

Věta: Posloupnost je klesající právě tehdy, když



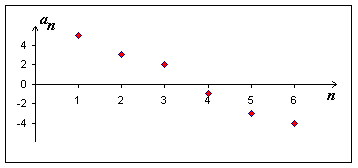Příklady:

{ 1, 1/2, 1/3, 1/4, 1/5, ... }
an = 3/n2 + 1,3
an+2 = 2an+1 - an ,  a1 = 1, a2 = 0

3. nerostoucí posloupnost

Definice: Posloupnost (an) se nazývá nerostoucí právě tehdy, když

 

Věta: Posloupnost je nerostoucí právě tehdy, když



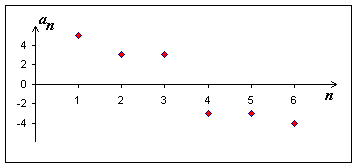Příklady:

{ 1, 1, 1, 1, 1, ... }
an = 3/n2 + 1,3
an+1 = an - 3,  a1 = 1

4. neklesající posloupnost

Definice: Posloupnost (an) se nazývá neklesající právě tehdy, když

 

Věta: Posloupnost je neklesající právě tehdy, když



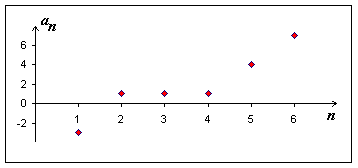Příklady:

{ 0, 1, 1, 2, 2, 3, 3, 4, ... }
an = 2n
an+2 = an+1 + an,  a1 = 1, a2 = 1


Omezenost posloupnosti


1. shora omezená posloupnost

Definice: Řekneme, že posloupnost (an) je shora omezená právě tehdy, když



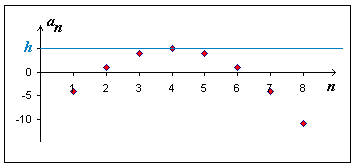Příklady:

{ 1, 0, -1, -2, -3, ... }
an = -2n
an = an-1 - 23 ,  a1 = 1

2. zdola omezená posloupnost

Definice: Řekneme, že posloupnost (an) je zdola omezená právě tehdy, když



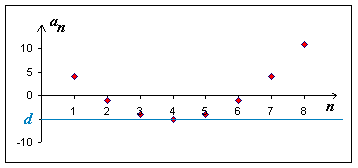Příklady:

{ -1, 1, 3, 5, 7, ... }
an = 5n2 - 13
an = an-1 + 5 ,  a1 = 1

3. omezená posloupnost

Definice: Řekneme, že posloupnost (an) je omezená právě tehdy, když je shora i zdola omezená, tedy když



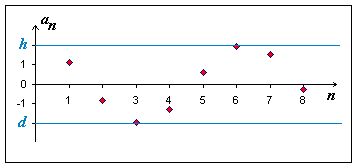Příklady:

{ -1, 1, -1, 1, -1, ... }
an = sin(n)
an+2 = (an+1 + an)/2,  a1 = -1, a2 = 1

Příklady

posloupnost rostoucí, klesající

1. Rozhodněte, které z následujících posloupností jsou rostoucí, které klesající a které nejsou ani rostoucí ani klesající:

a)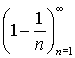
b)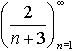
c)