Spojitost funkce v bodě a na intervalu
Definice:
Řekneme, že funkce f je spojitá v bodě a, jestliže
"e>0 $d>0 "xÎR platí xÎU(a,d) Þ f(x)ÎU(f(a),e)
|
|
Slovní popis: Řekneme, že funkce f je spojitá
v bodě a, jestliže k libovolně zvolenému okolí bodu f(a)
existuje takové okolí bodu a, že pro všechna x z tohoto okolí bodu a patří hodnoty f(x) do zvoleného okolí bodu f(a).
|
Definice:
Řekneme, že funkce f je spojitá v bodě a zleva, jestliže
"e>0 $d>0 "xÎR platí xÎU-(a,d) Þ f(x)ÎU(f(a),e)
|
|
Slovní popis: Řekneme, že funkce f je spojitá
v bodě a zleva, jestliže k libovolně zvolenému okolí bodu f(a)
existuje takové levé okolí bodu a, že pro všechna x z tohoto okolí bodu a patří hodnoty f(x) do zvoleného okolí bodu f(a).
|
Definice:
Řekneme, že funkce f je spojitá v bodě a zprava, jestliže
"e>0 $d>0 "xÎR platí xÎU+(a,d) Þ f(x)ÎU(f(a),e)
|
|
Slovní popis: Řekneme, že funkce f je spojitá
v bodě a zprava, jestliže k libovolně zvolenému okolí bodu f(a)
existuje takové pravé okolí bodu a, že pro všechna x z tohoto okolí bodu a patří hodnoty f(x) do zvoleného okolí bodu f(a).
|
Definice:
Řekneme, že funkce f je spojitá v otevřeném intervalu (a,b), je-li spojitá v každém bodě tohoto intervalu.
Definice:
Řekneme, že funkce f je spojitá v uzavřeném intervalu áa,bñ, je-li spojitá v (a,b) a v bodě a je spojitá zprava a v bodě b je spojitá zleva.
Několik příkladů pro lepší objasnění pojmu spojitost funkce v bodě.
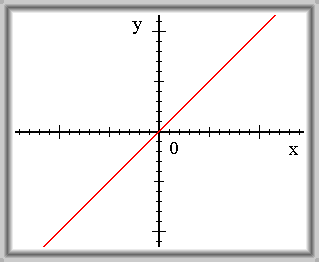 |
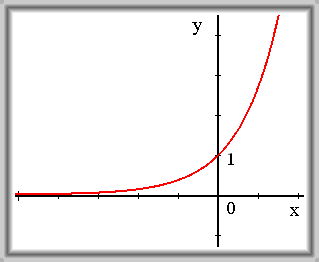 |
| f(x) = x f je spojitá v 0 |
f(x) = ex f je spojitá v 0 |
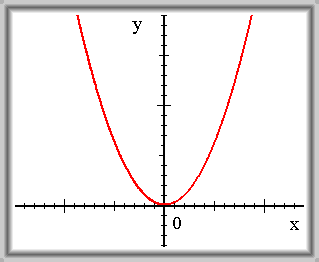 |
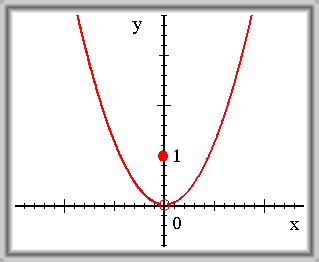 |
| f(x) = x2 f je spojitá v 0 |
f(x) = 1 pro
x=0 f(x) = x2 pro xÎR\{0} f není spojitá v 0 |