Vlastní limita funkce v nevlastním bodě
Definice:
Řekneme, že funkce f má v bodě +¥ limitu AÎR právě tehdy, když
"e>0 $x0ÎR "xÎR platí x>x0 Þ | f(x)-A |<e
|
|
Slovní vysvětlení:
Pro libovolné kladné číslo e
existuje reálné číslo
x0 takové, že pro každé reálné
číslo x>x0
leží f(x) v e-okolí čísla A. |
Matematický zápis:
Čteme: Limita funkce f pro x blížící se k +¥ je rovna A
Obrázek:
Definice:
Řekneme, že funkce f má v bodě -¥ limitu AÎR právě tehdy, když
"e>0 $x0ÎR "xÎR platí x<x0 Þ | f(x)-A |<e
|
|
Slovní vysvětlení:
Pro libovolné kladné číslo
e
existuje reálné číslo
x0 takové, že pro každé reálné
číslo x<x0 leží f(x) v e-okolí čísla A. |
Matematický zápis:
Čteme: Limita funkce f pro x blížící se k -¥ je rovna A
Obrázek:
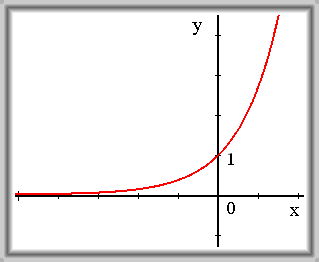
Názornou představu lze získat z následujících grafů funkcí
 |
 |
|
f(x) = ex
|
f(x)
= 1/x
|
 |
 |
|
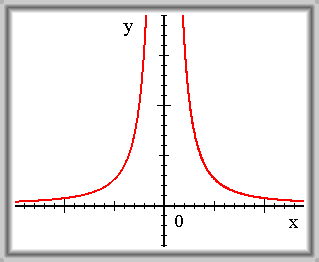
f(x)
= 1/x2
|
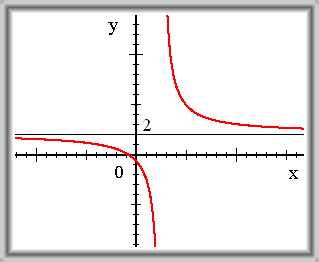
f(x)
= (2x+2)/(x-2.5)
|
