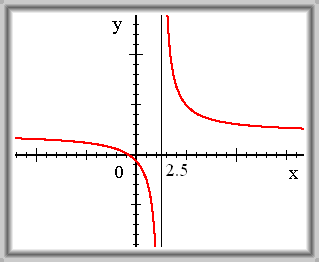
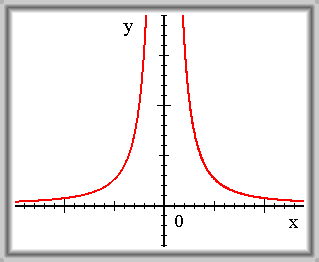
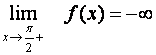Nevlastní limita funkce ve vlastním bodě
Definice:
Řekneme, že funkce f má v bodě cÎR limitu +¥ právě tehdy, když
"K>0 $d>0 "xÎR xÎP(c,d) Þ K < f(x)
|
|
Slovní popis: Ke každému číslu K
existuje kladné číslo d takové, že pro každé x z prstencového d-okolí
bodu c je f(x)>K. |
Matematický zápis:
![]()
Čteme: Limita funkce f pro x blížící se k c je rovna +¥
Definice:
Řekneme, že funkce f má v bodě cÎR limitu -¥ právě tehdy, když
"K<0 $d>0 "xÎR xÎP(c,d) Þ f(x) < K
|
|
Slovní popis: Ke každému číslu K
existuje kladné číslo d
takové, že pro každé x z prstencového d-okolí
bodu c je f(x)<K. |
Matematický zápis:
![]()
Čteme: Limita funkce f pro x blížící se k c je rovna -¥
Definice:
Řekneme, že funkce f má v bodě cÎR limitu +¥ zprava právě tehdy, když
"K>0 $d>0 "xÎR xÎP+(c,d) Þ K < f(x)
|
|
Slovní popis: Ke každému číslu K
existuje kladné číslo d takové, že pro každé x z
pravého prstencového d-okolí
bodu c je f(x)>K. |
Matematický zápis:
![]()
Čteme: Limita funkce f pro x blížící se k c zprava je rovna +¥
Definice:
funkce f má v bodě cÎR limitu +¥ zleva právě tehdy, kdyžŘekneme, že
"K>0 $d>0 "xÎR xÎP-(c,d) Þ K < f(x)
|
|
Slovní popis: Ke každému číslu K
existuje kladné číslo d takové, že pro každé x z
levého prstencového d-okolí
bodu c je f(x)>K. |
Matematický zápis:
![]()
Čteme: Limita funkce f pro x blížící se k c zleva je rovna +¥
Definice:
funkce f má v bodě cÎR limitu -¥ zprava právě tehdy, kdyžŘekneme, že
"K<0 $d>0 "xÎR xÎP
+(c,d) Þ f(x) < K
|
|
Slovní popis: Ke každému číslu K
existuje kladné číslo d takové, že pro každé x z
pravého prstencového d-okolí
bodu c je f(x)<K. |
Matematický zápis:
![]()
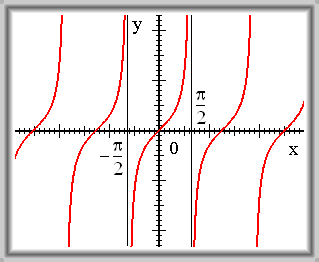
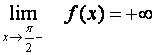 a
a