Základní kombinatorická pravidla
Úlohy
Úloha 1.1
Určete počet všech trojciferných přirozených čísel,
a) v jejichž dekadickém zápisu se každá číslice vyskytuje nejvýše jednou;
b) v jejichž dekadickém zápisu se nějaká číslice vyskytuje alespoň dvakrát.
 a) Postupně určete, kolik různých cifer může být na místě stovek, desítek a jednotek.
a) Postupně určete, kolik různých cifer může být na místě stovek, desítek a jednotek.
b) Použijte kombinatorické pravidlo součtu.

Výsledky:
a) 9 · 9 · 8 = 648

b) 900 − 648 = 252

a)
možnosti pro první číslici: 1 až 9
.... 9 možností;
možnosti pro druhou číslici: 0 až 9, ale bez té číslice, která byla vybrána pro první cifru
.... 10 − 1 = 9 možností;
možnosti pro třetí číslici: 0 až 9, ale bez číslic, které byly vybrány pro první a druhou cifru
.... 10 − 2 = 8 možností.
Podle kombinatorického pravidla součinu je tedy celkem 9 · 9 · 8 = 648 takových čísel.
b)
Všech trojciferných čísel je 900 (čísla 100 až 999), z toho čísel, v jejichž dekadickém zápisu se
každá číslice vyskytuje nejvýše jednou, je 648 – viz případ a). Zbývá tedy
900 − 648 čísel,
v jejichž dekadickém zápisu se nějaká číslice opakuje alespoň dvakrát.
Úloha 1.2
Určete, kolika způsoby lze na šachovnici 8 × 8 vybrat dvě různobarevná
pole tak, aby obě neležela v téže řadě ani v témže sloupci.

Výsledek: 32 · 24 =
768

Na šachovnici je 32 tmavých a 32 světlých polí. Nezáleží na tom, jestli jako
první vybereme světlé pole nebo tmavé pole, situace je symetrická.
Tmavé pole můžeme vybrat libovolně, máme tedy 32 možností. S vybraným
polem jsou ve stejné řadě 4 světlá pole a stejně tak i ve sloupci.
Pro výběr světlého pole proto zbývá
32 − 8 = 24 možností.
Podle kombinatorického pravidla součinu je
celkem 32 · 24 = 768 způsobů,
jak vybrat dvě pole podle podmínek zadání.
Úloha 1.3
Určete, kolik dvojjazyčných slovníků je třeba k tomu, aby byla zajištěna
možnost přímého překladu z anglického, francouzského, německého a ruského jazyka
do každého z nich.

Výsledek: 4 · 3 = 12
Úloha 1.4
Spočtěte, kolik čísel z množiny {1, 2, …, 100 000} je:
a) dělitelných 7;
b) dělitelných 5 nebo 11;
*c) dělitelných 6 nebo 10 nebo 15.
d) Jak se změní výsledek v případě, že uvažujeme čísla z množiny {0, 1, 2, …, 100 000}?

Výsledky:
a) 14 285;

b) 27 272;

c) 26 666;

d) Hledané počty se zvětší o jedna.

a) Každé sedmé číslo je dělitelné sedmi, proto je jejich počet
nejbližší celé číslo menší než 100 000 / 7,
tj. 14 285.
b) Každé páté číslo je dělitelné pěti, každé jedenácté je dělitelné jedenácti a každé
pětapadesáté je dělitelné pěti i jedenácti.
Označme množinu čísel dělitelných pěti P a množinu čísel dělitelných jedenácti J.
|P| = 100 000 / 5 = 20 000 (počet čísel z dané množiny dělitelných pěti);
|J| = [100 000 / 11] = 9 090 (počet čísel z dané množiny dělitelných jedenácti);
|P ∩ J| = [100 000 / 55] = 1 818 (počet čísel z dané množiny dělitelných pěti i jedenácti).
Výsledkem je počet prvků množiny P ∪ J:
|P ∪ J| = |P| + |J| − |P ∩ J|
= 20 000 + 9 090 − 1 818 = 27 272.
c) Označme množinu čísel dělitelných šesti A6,
množinu čísel dělitelných deseti A10
a množinu čísel dělitelných patnácti A15
(všechny jsou podmnožiny množiny {1, 2, …, 100 000}).
Počet čísel, která jsou dělitelná šesti, deseti nebo patnácti, odpovídá počtu
prvků množiny A6 ∪ A10 ∪ A15.
|A6 ∪ A10 ∪ A15|
= |A6| + |A10| + |A15| − |A6 ∩ A10|
− |A6 ∩ A15| − |A10 ∩ A15|
+ |A6 ∩ A10 ∩ A15|
|A6| = [100 000 / 6] = 16 666
|A10| = 100 000 / 10 = 10 000
|A15| = [100 000 / 15] = 6 666
|A6 ∩ A10| = [100 000 / nsn(6, 10)] = [100 000 / 30] = 3 333
|A6 ∩ A15| = [100 000 / nsn(6, 15)] = [100 000 / 30] = 3 333
|A10 ∩ A15| = [100 000 / nsn(10, 15)] = [100 000 / 30] = 3 333
|A6 ∩ A10 ∩ A15|
= [100 000 / nsn(6, 10, 15)] = [100 000 / 30] = 3 333
|A6 ∪ A10 ∪ A15| = 16 666 + 10 000 + 6 666
− 3 333 − 3 333 − 3 333 + 3 333 = 26 666
(nsn(x, y) znamená nejmenší společný násobek čísel x, y)
d) Přidaná nula je dělitelná každým nenulovým číslem, tedy také čísly 7, 5, 11, 6, 10 a 15.
Úloha 1.5
V košíku je 12 jablek a 10 hrušek. Petr si má z něho vybrat buď jablko,
anebo hrušku tak, aby Věra, která si po něm vybere jedno jablko a jednu hrušku, měla
co největší možnost výběru. Určete, co si má vybrat Petr.

Výsledek: jablko

Když si Petr vybere jablko, zůstane v košíku 11 jablek a 10 hrušek, tj. 11 · 10 = 110 možností výběru jednoho jablka a jedné hrušky.
Když si Petr vybere hrušku, zůstane v košíku 12 jablek a 9 hrušek, tj. 12 · 9 = 108 možností výběru jednoho jablka a jedné hrušky.
110 > 108, správná odpověď je tedy jablko.
Úloha 1.6
Na vrchol hory vedou čtyři turistické cesty a lanovka.
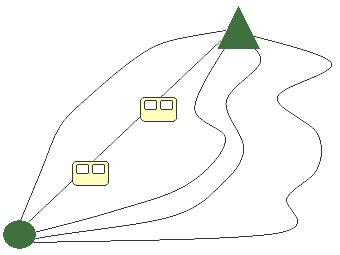
Určete počet způsobů, kterými je možno se dostat
a) na vrchol a zpět;
b) na vrchol a zpět tak, aby zpáteční cesta byla jiná než cesta na vrchol;
c) na vrchol a zpět tak, aby aspoň jednou byla použita lanovka;
d) na vrchol a zpět tak, aby lanovka byla použita právě jednou.

Výsledky:
a) 25, b) 20, c) 9, d) 8

a) 5 (nahoru libovolně) · 5 (dolů libovolně) = 25;
b) 5 (nahoru libovolně) · 4 (dolů jinak) = 20;
c) 1 (nahoru lanovkou) · 4 (dolů po cestě) + 4 (nahoru po cestě) · 1 (dolů lanovkou)
+ 1 (nahoru i dolů lanovkou) = 9;
d) 1 (nahoru lanovkou) · 4 (dolů po cestě) + 4 (nahoru po cestě) · 1 (dolů lanovkou) = 8.
Úloha 1.7
Určete počet všech čtyřciferných přirozených čísel, v jejichž dekadickém
zápisu není nula a ze zbývajících devíti číslic se v něm každá vyskytuje nejvýše jednou.
Kolik z těchto čísel je větších než 9 000?
Kolik je menších než 3 000?

Výsledky:
3 024; 336; 672

9 · 8 · 7 · 6 = 3 024 (postup je podobný jako v úloze 1);
1 · 8 · 7 · 6 = 336 (na místě tisíců může být pouze číslice 9, tj. 1 možnost, další postup zůstává stejný);
2 · 8 · 7 · 6 = 672 (na místě tisíců mohou být pouze číslice 1 a 2, tj. 2 možnosti, další postup zůstává stejný).
Úloha 1.8
Určete počet všech čtyřciferných přirozených čísel, jejichž dekadický
zápis je složen z číslic 1, 2, 3, 4, 5 (každá se může opakovat), která jsou dělitelná
a) pěti,
b) dvěma,
c) čtyřmi.

Výsledky:
a) 125; b) 250; c) 125

a) aby bylo výsledné číslo dělitelné pěti, může být na místě jednotek pouze číslice 5;
na ostatních místech může být libovolná číslice 1 až 5
.... 5 · 5 · 5 · 1 = 125
b) aby bylo výsledné číslo dělitelné dvěma, mohou být na místě jednotek pouze číslice 2 a 4;
na ostatních místech může být libovolná číslice 1 až 5
.... 5 · 5 · 5 · 2 = 250
c) přirozené číslo je dělitelné čtyřmi, pokud je jeho poslední dvojčíslí dělitelné čtyřmi.
Pro sestavení posledního dvojčíslí máme tedy pět možností: 12, 24, 32, 44, 52. Na zbylých dvou místech může být libovolná číslice 1 až 5.
.... 5 · 5 · (5) = 125
Úloha 1.9
Z místa A do místa B vede pět cest, z místa B do místa C vedou dvě cesty
a z místa A do místa C vede jedna cesta (viz obrázek).
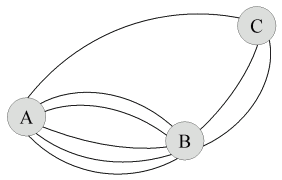
Určete, kolika různými způsoby lze vykonat cestu
a) z místa A do místa C přes místo B;
b) z místa A do místa C (jakkoli);
d) z místa A do místa C (jakkoli) a potom zpět do místa B (přímo),
jestliže každým místem můžete projít nejvýše jednou (není možné se vracet).

Výsledky:
a) 10; b) 11; c) 22

a) Přímá cesta z místa A do místa C se nepoužije, postup řešení je tedy stejný
jako v příkladu 2.
Počet cest z místa A do místa B je pět, počet cest z místa B do místa C jsou dvě.
Celkem je tedy 5 · 2 = 10 způsobů, jak jít z místa A do místa C přes místo B.
b) Využijeme kombinatorické pravidlo součtu: z místa A do místa C přes místo B se dostaneme deseti způsoby (minulý případ),
přímá cesta je jen jedna. Celkem je tedy 10 + 1 = 11 způsobů, jak jít z místa A do místa C.
c) Využijeme kombinatorické pravidlo součinu: z místa A do místa C se dostaneme 11 způsoby (minulý případ),
ke každému z nich můžeme vybrat jednu ze dvou přímých cest z místa C do místa B.
Celkem je tedy 11 · 2 = 22 způsobů, jak vybrat cestu podle zadání.
Úloha 1.10
Je dán čtverec ABCD a na každé jeho straně n vnitřních bodů.
Určete počet trojúhelníků
s vrcholy v těch bodech, jejichž žádná strana neleží ve straně čtverce ABCD.

Výsledek: 4n3

Pro každý trojúhelník splňující zadání platí, že jeho vrcholy leží na třech stranách čtverce ABCD.
Pro n = 2 vypadá jeden z trojúhelníků takto:
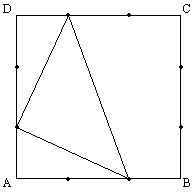
Všechny trojúhelníky tedy můžeme rozdělit na čtyři skupiny podle toho, která strana čtverce zůstane
"nevyužitá". Dále nás zajímá, kolik je trojúhelníků v jedné takové skupině. Na každé ze tří stran
čtverce vybíráme jeden z n bodů, můžeme tedy sestavit n3 trojúhelníků.
Hledaný počet je proto 4 · n3.
Úloha 1.11
Určete, kolika způsoby se lze dostat z A do B, cestujeme-li po cestách
zobrazené sítě a nikdy se nevracíme směrem k místu A. Jedna z možných cest je zobrazena.

 Pro výpočet jsou zajímavé pouze cesty, které
vedou zleva doprava; svislé cesty se k nim doplní jednoznačně.
Pro výpočet jsou zajímavé pouze cesty, které
vedou zleva doprava; svislé cesty se k nim doplní jednoznačně.

výsledek: 36

Pro výpočet jsou zajímavé pouze cesty, které vedou zleva doprava. Když vybereme
v každém ze šesti úseků jednu ze tří takových cest, určíme tak vlastně jednu konkrétní trasu z A do B;
svislé cesty se doplní jednoznačně. Každé tři "křižovatky", které jsou v síti nad sebou,
tak můžeme pokládat za jediný bod, ve kterém se rozhodujeme o dalším pokračování trasy.
Obrázek pak můžeme překreslit následovně:
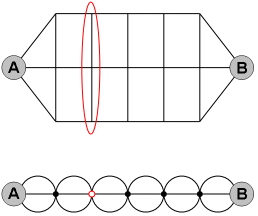
Dál už je postup stejný, jako v příkladu 2.
Z A do B se tedy lze dostat
3 · 3 · 3 · 3 · 3 · 3 = 36
způsoby.
![]() a) Postupně určete, kolik různých cifer může být na místě stovek, desítek a jednotek.
a) Postupně určete, kolik různých cifer může být na místě stovek, desítek a jednotek.![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()

![]() Pro výpočet jsou zajímavé pouze cesty, které
vedou zleva doprava; svislé cesty se k nim doplní jednoznačně.
Pro výpočet jsou zajímavé pouze cesty, které
vedou zleva doprava; svislé cesty se k nim doplní jednoznačně.
![]()

