Existuje několik způsobů rozkladu mnohočlenu:
1. Vytknutí společného mnohočlenu před závorku

Příklad
Rozlož mnohočlen vhodným vytknutím před závorku:
a)
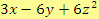Řešení


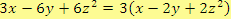
b)
Řešení


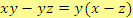
c)
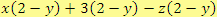Řešení


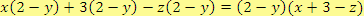
d)
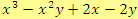Řešení



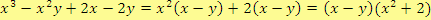2. Rozklad pomocí vzorce
Většinou používáme následující vzorce (s některými už jsme se setkali u součinu mnohočlenů):

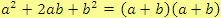
Pozn. Abychom dodrželi přesné znění definice rozkladu mnohočlenu, tedy že mnohočlen vyjádříme jako součin jednodušších mnohočlenů, měli bychom správně psát např. . Pro větší přehlednost ale budeme i v dalším textu používat zkrácený zápis, tedy .

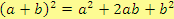
Příklad[nahoru]
Rozlož mnohočlen s využitím vzorců:
a)
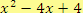Řešení


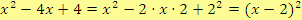
b)
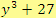Řešení


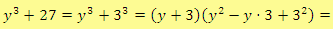
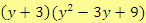
c)
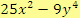Řešení


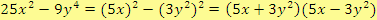
d)
Řešení




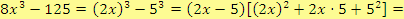
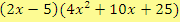3. Rozklad kvadratického trojčlenu
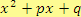
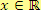
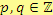
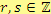
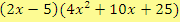
V tomto případě chceme rozložit kvadratický trojčlen , kde , , na součin dvou lineárních dvojčlenů , kde . Ne vždy taková čísla , existují. Pokud však existují, tak pro ně musí platit:
.
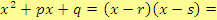
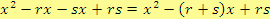
To znamená, že .
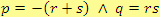
Z těchto dvou podmínek určíme čísla , , pokud existují.

Pozn. Uvedené vztahy platí i v případě, že p, q, r, s jsou reálná čísla.

Příklad[nahoru]
Rozlož kvadratický trojčlen na součin dvou lineárních dvojčlenů s celočíselnými koeficienty:
a)
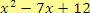Řešení
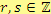
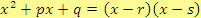
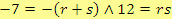
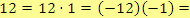
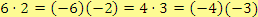
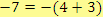
Pokud existují taková, že , tak pro ně musí platit, že . Aby byla splněna druhá podmínka, přichází v úvahu tyto možnosti: . První podmínce vyhovuje možnost , tj. .
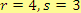
Výsledek je tedy: .

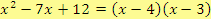
b)
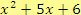Řešení
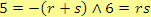
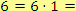
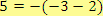
Hledáme čísla , taková, že . Druhé podmínce vyhovuje . A první podmínka je splněna pro , tj. .
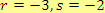
Výsledek je tedy: .

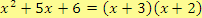
c)
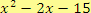Řešení
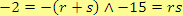
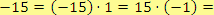
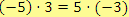
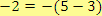
Hledáme čísla , taková, že . Druhé podmínce vyhovuje . A první podmínka je splněna pro , tj. .
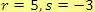
Výsledek je tedy: .

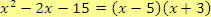
d)
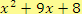Řešení
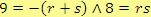
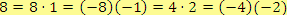
Hledáme čísla , taková, že . Druhé podmínce vyhovuje . A první podmínka je splněna pro , tj. .
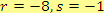
Výsledek je tedy: .


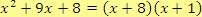
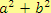
Rozklad mnohočlenu není vždycky patrný na první pohled. Někdy mnohočlen dokonce nelze v oboru reálných čísel rozložit vůbec (např. mnohočlen ). Přesto však je rozklad mnohočlenu užitečný, např. při počítání výrazů se zlomky.

Cvičení k této kapitole.[nahoru]