Obecná definice limity

    Na první pohled je zjevné, že definice limity se liší podle toho, zda c a A jsou reálná čísla nebo nevlastní body. To způsobuje určité problémy při důkazu některých vět o limitách, neboť je nutné dokazovat každý případ zvlášť. Řešením těchto obtíží může být taková definice limity funkce, která nebude rozlišovat, zda c a A jsou reálná čísla nebo nevlastní body. Taková definice skutečně existuje. Abychom ji však mohli používat, musíme rozšířit definici okolí bodu i pro nevlastní body (tj. pro +Ą a -Ą).

V následujících definicích je e ÎR, e>0.

Definice:

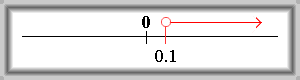
Epsilonovým okolím bodu +Ą rozumíme množinu {xÎR| 1/e<x}.

Značíme: U(+Ą,e)

Obrázek

Hodnota čísla e

   e = 10
   e = 1
   e = 0.5

Definice:

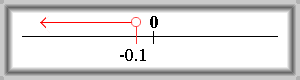
Epsilonovým okolím bodu -Ą rozumíme množinu {xÎR| x<-1/e}.

Značíme: U(-Ą,e)

Obrázek

Hodnota čísla e

   e = 10
   e = 1
   e = 0.5

Definice:

Prstencovým epsilonovým okolím bodu +Ą rozumíme množinu {xÎR|  1/e<x}.

Značíme: P(+Ą,e)

Obrázek

Hodnota čísla e

   e = 10
   e = 1
   e = 0.5

Definice:

Prstencovým epsilonovým okolím bodu -Ą rozumíme množinu {xÎR| x<-1/e}.

Značíme: P(-Ą,e)

Obrázek

Hodnota čísla e

   e = 10
   e = 1
   e = 0.5

 
Příklady:

P(-Ą,2) = {xÎR| x<-1/2} = (-Ą,-1/2)

U(+Ą,2) = {xÎR| 1/2<x} = (1/2,+Ą)

U(+Ą,0.1) = {xÎR| 10<x} = (10,+Ą)

 

Proč je v definicích použito 1/e ?

Důvod je tento: Pro okolí vlastního bodu platí, že pro menší hodnotu epsilon získáme podmnožinu předchozího okolí. Např. P(a,1) Ě P(a,2). Stejnou vlastnost požadujeme i od okolí nevlastního bodu. A proto je v definici použito 1/e. Př. U(+Ą,0.1) Ě U(+Ą,2).

Shrnutí

U(+Ą,e) = P(+Ą,e) = {xÎR| 1/e<x}
U(-Ą,e) = P(-Ą,e) = {xÎR| x<-1/e}
 

    Limitu funkce f pak můžeme definovat bez ohledu na skutečnost, zda c a A jsou reálná čísla nebo nevlastní body.

Definice:

Řekneme, že funkce f má v bodě c limitu A právě tehdy, když

"e>0 $d>0 "xÎR platí xÎ P(c,d) Ţ  f(x)ÎU(A,e)
Čísla c a A mohou být reálná či +Ą nebo -Ą.