Středová souměrnost

Tato metoda je speciálním případem metody otočení (pro velikost úhlu otočení α = 180°). Její princip proto plyne z principu metody otočení. Je-li v rovině dán bod S, úhel o velikosti α = 180° a dvě různé čáry m, n, pak všechny body čáry m, které po otočení o přímý úhel ve zvoleném smyslu budou ležet na čáře n, dostaneme jako body průniku čáry n a čáry m′ vzniklé otočením čáry m.

Příklad 1

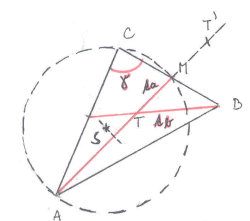
Zadání: Sestrojte trojúhelník ABC, je-li dáno: γ = 82°, ta = 4,7cm, tb = 3,5cm.

Řešení:

Rozbor: Daná úloha je nepolohová. Převedeme ji v polohovou úlohu se dvěma neznámými body B, C umístěním těžnice AM dané délky |AM| = t_a (M je střed strany BC) na zvolenou polopřímku AX. Nechť T′ je obraz těžiště T trojúhelníka ABC ve středové souměrnosti podle středu M (|AT| = |TT′| = ²/₃ • t_a, |AM| = t_a). Obrazem ΔMTB v tomto zobrazení je ΔMT′C, takže platí ΔMT′C  ΔMTB a odtud plyne, že |CT′| = |BT| = ²/₃ • t_b. Bod C musí proto splňovat následující dvě podmínky: od bodu T ′ má vzdálenost ²/₃ • t_b a leží na kružnicovém oblouku, z něhož je vidět úsečku AM v zorném úhlu dané velikosti γ. Bod B musí vyhovovat těmto podmínkám: od těžiště T má vzdálenost ²/₃ • t_b, leží na polopřímce CM.

Řešení v AutoCADu:    

Zkouška: Z rozboru vyplývá, že sestrojený trojúhelník ΔABC má všechny vlastnosti požadované v zadání úlohy.

Diskuse: Při daném číselném zadání prvků existuje právě jedno řešení.

Příklad 2

Zadání: Je dána úsečka AA1, |AA1| = 4,5cm. Sestrojte všechny pravoúhlé trojúhelníky ABC s pravým úhlem při vrcholu C, v nichž AA1 je těžnicí ta a tb = 6cm.

Řešení:

Rozbor: Daná úloha je polohová se dvěma neznámými body B, C, které jsou krajními body úsečky, která má střed A₁. Nechť T′ je obraz těžiště T trojúhelníka ABC ve středové souměrnosti podle středu A₁ (|A₁T| = |TT′| = ²/₃ • t_a , |AA₁| = t_a). Bod C musí splňovat následující dvě podmínky: od bodu T ′ má vzdálenost ²/₃ • t_b a leží na Thaletově kružnici t s průměrem AA₁. Bod B musí vyhovovat těmto podmínkám: od těžiště T má vzdálenost ²/₃ • t_b, leží na polopřímce CA₁.

Řešení v AutoCADu:    

Zkouška: Z rozboru vyplývá, že sestrojený trojúhelník ΔABC má všechny vlastnosti požadované v zadání úlohy.

Diskuse: Protože mají kružnice k′ a t společné dva body, má úloha právě dvě řešení.

Příklad 3

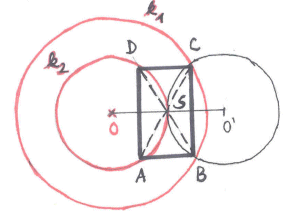
Zadání: Jsou dány dvě soustředné kružnice k1(O;r1), k2(O;r2), r1 > r2, a bod S ležící na menší z nich. Sestrojte rovnoběžník ABCD se středem S, jehož vrcholy leží na daných kružnicích.

Řešení:

Rozbor: Úloha je nepolohová, převedeme ji na úlohu polohovou umístěním bodu S na kružnici k₂ se čtyřmi neznámými body A, B, C, D. Bod S je středem rovnoběžníku ABCD, tedy je středem úsečky AC i BD. Z toho vyplývá, že bod C je obrazem bodu A ve středové souměrnosti se středem S a bod B je obrazem bodu D ve středové souměrnosti se středem S. Jestliže bod A leží na kružnici k₂, musí bod C jako jeho obraz ležet na obrazu k₂′ kružnice k₂ ve středové souměrnosti se středem S, proto C  k₂′  k₁. Bod A je pak obrazem bodu C. Obdobně platí pro dvojici bodů B, D.

Řešení v AutoCADu:    

Zkouška: Čtyřúhelník ABCD je rovnoběžník, neboť z definice středové souměrnosti plyne, že |SA| = |SC|, |SB| = |SD|. A pro všechny vrcholy platí z rozboru, že leží na daných kružnicích. Tedy řešení splňuje všechny požadavky úlohy.

Diskuse: Úloha má řešení pouze tehdy, když se kružnice k₁ a k₂′ protnou. To nastane pro případ, kdy r₂ > ¹/₃ • r₁. Pokud má úloha řešení je to řešení jediné.