Zobrazení - společné vlastnosti a příklady

Rys 1 - Přímé a nepřímé zobrazení

Demonstrace nepřímého zobrazení. Modrá kružnice a modrý trojúhelník jsou zobrazeny v osové souměrnosti s osou o.

Rys je animovaný, po jeho otevření se začnou automaticky pohybovat dva body (jeden po trojúhelníku, druhý po kružnici) a spolu s nimi i jejich obrazy. Všimněte si, že bod na modré kružnici se pohybuje po směru hodinových ručiček, zatímco jeho obraz na červené kružnici se pohybuje proti směru hodinových ručiček.

Podobně bod pohybující se po modrém trojúhelníku postupně přes vrcholy A, B a C vždy vrcholu "zatáčí" vpravo, zatímco jeho obraz postupující přes vrcholy ve stejném pořadí "zatáčí" vlevo.

Obdobná demonstrace přímého zobrazení, v tomto případě středové souměrnosti.

Rys 3 - Skládání osových souměrností

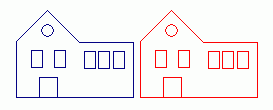
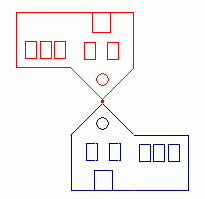
Na rysu máme obrázek modrého domku. Světle šedý domek je jeho obrazem v osové souměrnosti podle přímky o1. Nakonec červený domek je obrazem šedého v osové souměrnosti podle přímky o2.

Tedy červený domek vznikne z modrého složením dvou osových souměrností.

Měňte vzájemnou polohu os o1 a o2 (přímky se dají přesunout tažením svého určujícího bodu). Sledujte při tom, jak se mění poloha červeného domku, výsledku složeného zobrazení. Pokuste se dosáhnout např. následujících poloh modrého a červeného domku:

Zkuste složením osových souměrností nahradit ostatní shodná zobrazení, která znáte (identita, posunutí, středová souměrnost, otočení, posunutá osová souměrnost).

Jakým způsobem lze nahradit identitu?

Složením dvou osových souměrností, jejichž osy jsou totožné (o1 = o2).

Jakým způsobem lze nahradit posunutí?

Složením dvou osových souměrností, jejichž osy jsou rovnoběžné (o1 = o2).

Jak závisí velikost a směr vektoru posunutí na poloze os o1 a o2?

Velikost vektoru posunutí je dvojnásobkem vzdálenosti os o1 a o2 a jeho směr je kolmý na osy o1 a o2.

Jakým způsobem lze nahradit středovou souměrnost?

Složením dvou osových souměrností, jejichž osy jsou na sebe kolmé.

Jak otočení? Kde je jeho střed a jaká je velikost úhlu otočení?

Složením dvou osových souměrností, jejichž osy jsou na sebe různoběžné. Střed otočení je v průsečíku os, velikost úhlu otočení je dvojnásobkem velikosti úhlu, který svírají osy o1 a o2.

Jak lze nahradit posunutou osovou souměrnost?

Poznámka: Posunutá osová souměrnost je shodné zobrazení vzniklé složením osové souměrnosti a posunutí, je tedy určeno osou a orientovanou úsečkou.

Posunutou osovou souměrnost nelze získat složením dvou osových souměrností. Posunutá osová souměrnost je nepřímá shodnost, zatímco složením dvou osových souměrností (tedy nepřímých shodností) je vždy shodnost přímá.

Závěr:

Složením dvou osových souměrností lze nahradit libovolné posunutí, otočení, středovou souměrnost a identitu. Posunutá osová souměrnost se dá nahradit složením 3 osových souměrností.

Rys 4 - Kružnice

Jednoduchým opakujícím se rýsováním kružnic vznikl následující rys.

Pokuste se najít v rysu či jeho částech co nejvíce symetrií (osové, středové, otočení).

Rys 5 - Kruhová inverze

Na závěr této kapitoly ještě jeden rys na demonstraci kruhové inverze, jako příklad dalšího typu geometrického zobrazení, které ovšem není v základním učivu pro střední školy. Pomocí nástroje množina objektů jsou vytvořeny obrazy čtverce, trojúhelníka, přímky a kružnice v kruhové inverzi dané zvýrazněnou kružnicí.

Pohybujte jednotlivými objekty (čtverec, trojúhelník, kružnice, přímka), vně i uvnitř kružnice a sledujte jak se mění jejich obrazy. Hledejte samodružné body a přímky.

Rys 6 - Spirála

Rys vytvořený opakovaným použitím makra pro vepsání zmenšeného a pootočeného pětiúhelníka (tedy složení stejnolehlosti a otočení). Makro rozdělí strany pětiúhelníka v poměru 1:7 a takto vzniklé body pospojuje do nového, vepsaného pětiúhelníka.

Úloha 1

Je dán libovolný trojúhelník ABC a bod P1. Bod P2 je obrazem P1 ve středové souměrnosti se středem A, bod P3 je obrazem P2 ve středové souměrnosti se středem C a bod P4 je obraz bodu P3 podle středové souměrnosti se středem B.

Dokažte, že střed úsečky P1P4 je nezávislý na poloze bodu P1.

Nápověda: Složením dvou osových souměrností vznikne posunutí. Složením posunutí a středové souměrnosti je středová souměrnost.

Odkazy

• Shodná zobrazení v rovině - článek A. Vrby využívající Cabri Geometry.
• Neshodná zobrazení - výukové projekty pomocí Cabri Geometrie J. Vaníčka
• Tess - program pro tvorbu grafických symetrických vzorů (anglicky)
• Symmetry and Pattern - The Art of Oriental Carpets (Symetrie a vzory orientálních koberců)