Je dána přímka o. Osová souměrnost s osou o je shodné zobrazení O(o), které přiřazuje:
Velký modrý trojúhelník uprostřed rysu představuje zrcadla v kaleidoskopu. Uvnitř něj jsou tři malé vybarvené trojúhelníky (zelený, fialový a žlutý), ostatní vybarvené trojúhelníčky jsou jejich zrcadlové obrazy a obrazy těchto obrazů.
Zkuste pohybovat a měnit tvar tří trojúhelníků uvnitř "kaleidoskopu". Zkuste měnit samotný kaleidoskop (velký modrý trojúhelník). Výsledkem budou zajímavé měnící se symetrické vzory.
Zkuste rozlišit, které jsou první odrazy "skutečných" trojúhelníků, co jsou odrazy odrazů a ve kterých "zrcadlech" jsou zrcadleny.
Podobný kaleidoskop jako v předchozím rysu, tentokrát animovaný.
Červený bod je obrazem modrého bodu v osové souměrnosti podle dané přímky. Oba body mají zapnutou funkci zanechávání stopy.
Tažením modrého bodu zkuste namalovat různé symetrické obrázky (např. květinu, strom, vázu, obličej, dům či abstraktní ornament).
Poznámka: Několik nespojených čar lze namalovat tak, že se vypne stopa oběma bodům, přenesou se na nové místo a stopa se opět zapne. Na zapnutí / vypnutí stopy v CabriJava slouží třetí ikona zprava na panelu nástrojů. Nový obrázek lze začít dvojitým poklepáním myši na plochu rysu. Tím se obrázek překreslí a stopy se smažou.
Příklady jednoduchých osově souměrných obrázků namalovaných tímto způsobem:

Zkuste napsat své jméno (či jakýkoliv jiný text) červeně. Táhnout lze pouze modrým bodem, budete muset proto napsat své jméno zrcadlově. Výsledek může vypadat např. takto:
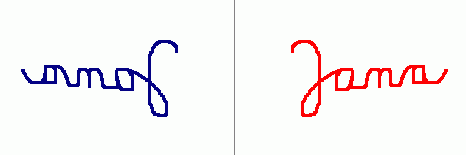
Tento rys je podobný předchozímu rysu, jen modrý bod má místo jednoho celkem tři souměrné obrazy podle dvou os.
Zkuste opět namalovat symetrické objekty či ornamenty či napsat text tak, aby některý jeho obraz byl čitelný běžným způsobem.
Máme dánu osovou souměrnost s osou o, přímku p a její obraz v dané souměrnosti označený p’.
Měňte polohu a směr přímky p a všimněte si, jak se při tom mění její obraz v osové souměrnosti s osou o. Kdy modrá přímka p splyne se svým obrazem - červenou přímkou p‘ a je tedy tzv. samodružná?
Když je přímka p kolmá na osu souměrnosti nebo je s ní totožná.
Kdy je přímka p přímkou samodružných bodů
Pokud je totožná s osou souměrnosti.
Kdy je přímka p rovnoběžná se svým obrazem?
Pokud je rovnoběžná s osou souměrnosti.
Na rysu jsou zobrazeny dva domky, modrý a červený. Červený domek je obrazem modrého domku v osové souměrnosti. Osa této souměrnosti je však skryta.
Pokuste se odhadnout polohu osy souměrnosti - přesuňte na její předpokládané místo přímku p. Nakonec se můžete přesvědčit, jak byl odhad přesný - stačí posunout konstrukci o dva kroky vpřed, čímž se zkonstruuje skutečná osa souměrnosti.
Následující rysy demonstrují řešení problému "úhel dopadu = úhel odrazu" pomocí osové souměrnosti na příkladě kulečníku. Analogický model se dá použít např. na odraz puku od mantinelu při hokeji a podobně.
Rysy ukazují geometrickou konstrukci dráhy červené koule tak, aby zasáhla modrou kouli s odrazem od jedné, dvou nebo tří stěn v daném pořadí (horní-pravá-dolní), například aby se vyhnula překážce - jiným koulím.
Existují pozice koulí, kdy taková dráha neexistuje, žáci mohou takové postavení zkusit najít a popsat. Například - v druhém případě modrou kouli nelze zvoleným způsobem zasáhnout, leží-li "nalevo" od přímky procházející červenou koulí a pravým horním rohem herní plochy.
Je dán rovnoramenný trojúhelník ABC (AB je základna).
Dokažte, že součet vzdáleností každého bodu X základny AB od přímek BC a AC je konstantní.
Pohybujte bodem X po základně. Ověřte, že naměřený součet vzdáleností od ramen se skutečně nemění.
Poznámka: Posunutím konstrukce o několik kroků vpřed lze zobrazit pomocnou konstrukci.
Řešení:
V důkazu využijeme znalostí o osové souměrnosti (podle strany AB):
Jsou dány dvě různé přímky o a p a kružnice k(O,r). Sestrojte úsečku XY tak, aby bod X ležel na kružnici k, bod Y na přímce p a aby osou úsečky XY byla přímka o.
Řešení:
Předpokládejme, že úloha má řešení. Protože přímka o je osou úsečky XY (půlí ji a je na ni kolmá), Y je obrazem X v osové souměrnosti podle o. Víme, že X leží na kružnici k, jeho obraz v osové souměrnosti podle o (bod Y) musí tedy ležet na k’, obrazu kružnice k podle stejné osové souměrnosti. Současně ze zadání víme, že Y leží na přímce p. Bod Y tedy dostaneme jako průsečík p a k’. Úloha má dvě, jedno, nebo žádné řešení.
Zkuste měnit zadané objekty (kružnici k a přímky p, q) a vytvořte situace, kdy úloha má jedno nebo žádné řešení. Popište, kdy to nastane.
Kružnice k1(S1,r1), k2(S2,r2) leží v opačných polorovinách s hraniční přímkou p.
Sestrojte kosočtverec ABCD tak, aby vrchol A ležel na k1, vrchol C na k2, vrcholy B a D na přímce p a délka úhlopříčky BD byla 5 cm.
Měňte vzájemnou polohu k1, k2 a p tak, aby úloha měla jedno, dvě nebo žádné řešení.
| [ zpět ] [ nahoru ] [ titulní stránka ] |
Poslední úprava této stránky: 2024-11-15 Zoran Bonuš |