Soustavy logaritmických rovnic
Při řešení soustav logaritmických rovnic musíme nejprve určit podmínky řešitelnosti. Podmínky budeme ověřovat již během výpočtu, jak je ukázáno v následujícím příkladu.
Řešte soustavu rovnic s neznámými x,y \in R:
- Výrazy v rovnici jsou definovány za podmínek x>0, ~y>0.
- Z druhé rovnice x-y=3 vyjádříme neznámou x:
x=3+y. - Do první rovnice \log x + \log y = 1 dosadíme za neznámou x výraz 3+y:
\log(3+y)+\log y = 1. - Z předchozí rovnice vypočteme neznámou y (viz řešení logaritmických rovnic):
y_1=2, ~y_2=-5. - Protože kořen y_2=-5 nesplňuje podmínku y>0, nemůže patřit do řešení soustavy rovnic.
- Neznánou x získáme z rovnice x=3+y dosazením y=2:
x=5 - Množina kořenů soustavy rovnic K=\{[5,2]\}.
Zápis řešení:
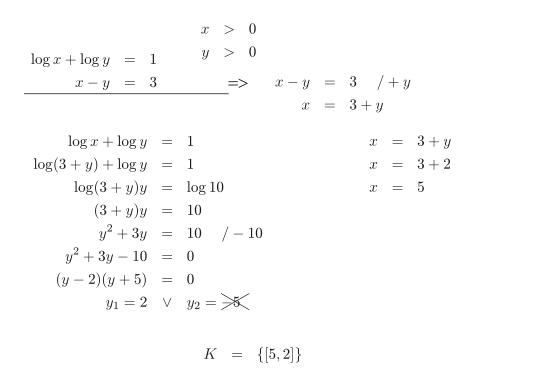
Řešte soustavu rovnic s neznámými x,y \in R:
- Výrazy v rovnici jsou definovány za podmínek x>0, ~y>0, ~x\neq 1, ~y \neq 1.
- Z první rovnice \log_3 x + \log_3 y = 5 vyjádříme výraz \log_3 x, který v následujícím kroku snadno dosadíme do druhé rovnice:
\log_3 x = 5 - \log_3 y. - Do druhé rovnice dosadíme za výraz \log_3 x výraz (5 - \log_3 y):
\frac{2(5 - \log_3 y)}{\log_3 y}-\frac{3\log_3 y}{5 - \log_3 y}=1 . - Z předchozí rovnice vypočteme neznámou y (viz řešení logaritmických rovnic):
y=9. - Neznámou x získáme z rovnice \log_3 x = 5 - \log_3 y dosazením y=9 (řešení logaritmické rovnice):
x=27 - Množina kořenů soustavy rovnic K=\{[27,9]\}.
Zápis řešení:
