Substituce
Některé exponenciální nerovnice nelze vyrešit porovnáním exponentů ani logaritmováním. Takové nerovnice se snažíme vhodnou substitucí převést na nerovnice, které už umíme vyřešit.
Pojem substituce jsme již zavedli při řešení exponenciálních rovnic. Zápis řešení i použité značení jsou tedy stejné.
Substituce za mocninu
Příklady, které ukážeme v této kapitole, se dají vždy řešit vhodnou substitucí nové neznámé za mocninu. V jednotlivých příkladech ukážeme, jak z řešení nerovnice s novou neznámou získáme původní řešení nerovnice.
Řešte nerovnici s neznámou x \in R:
- Definiční obor nerovnice D=R.
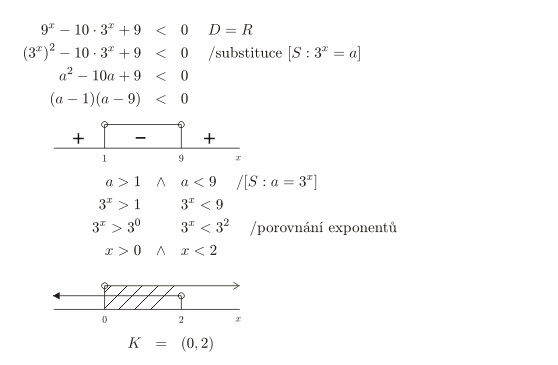
- Abychom mohli zavést substituci, musíme mocninu 9^x upravit: 9^x=(3^x)^2.
- V nerovnici (3^x)^2-10\cdot3^x+9 < 0 nahradíme všechny výrazy 3^x novou neznámou a.
- Nerovnici a^2-10a+9<0 s neznámou a \in R vyřešíme.
- Nerovnici převedeme na součinový tvar (a-1)(a-9)<0 a vyřešíme s pomocí číselné osy. Řešením je interval (1,9).
- Pro neznámou a tak dostáváme podmínky:
a>1 a zároveň a<9. - Zpětně nahradíme neznámou a výrazem 3^x.
- Pro neznámou x dostáváme podmínky:
3^x>1 a zároveň 3^x<9. - Nerovnice vyřešíme porovnáním exponentů:
x>0 a zároveň x<2. - Množinu kořenů určíme s pomocí číselné osy: K=(0,2).
Zápis řešení:
Řešte nerovnici s neznámou x \in R:
- Definiční obor nerovnice D=R.
- Abychom mohli zavést substituci, musíme mocninu 16^x upravit: 16^x=(4^x)^2.
- V nerovnici (4^x)^2-2\cdot4^x-8 \geq 0 nahradíme všechny výrazy 4^x novou neznámou a.
- Nerovnici a^2-2a-8 \geq 0 s neznámou a \in R vyřešíme.
- Nerovnici převedeme na součinový tvar (a+2)(a-4)\geq 0 a vyřešíme s pomocí číselné osy. Řešením je sjednocení intervalů (-\infty,-2>\cup<4,+\infty).
- Pro neznámou a tak dostáváme podmínky:
a\leq-2 nebo a\geq4. - Zpětně nahradíme neznámou a výrazem 4^x.
- Pro neznámou x dostáváme podmínky:
4^x\leq -2 nebo 4^x\geq 4. - Nerovnice vyřešíme porovnáním exponentů:
x\in \emptyset nebo x\geq 1. - Množina všech kořenů K=<1,+\infty).
Zápis řešení:

Řešte nerovnici s neznámou x \in R:
- Definiční obor nerovnice D=R.
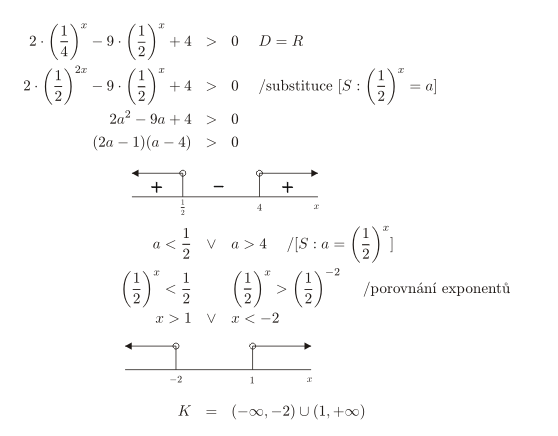
- Abychom mohli zavést substituci, musíme mocninu (\frac{1}{4})^x upravit: (\frac{1}{4})^x=(\frac{1}{2})^{2x}.
- V nerovnici 2\cdot (\frac{1}{2})^{2x}-9\cdot(\frac{1}{2})^x+4 > 0 nahradíme všechny výrazy (\frac{1}{2})^x novou neznámou a.
- Nerovnici 2a^2-9a+4 < 0 s neznámou a \in R vyřešíme.
- Nerovnici převedeme na součinový tvar (2a-1)(a-4) > 0 a vyřešíme s pomocí číselné osy. Řešením je sjednocení intervalů (-\infty,\frac{1}{2})\cup(4,+\infty).
- Pro neznámou a tak dostáváme podmínky:
a<\frac{1}{2} nebo a>4. - Zpětně nahradíme neznámou a výrazem (\frac{1}{2})^x.
- Pro neznámou x dostáváme podmínky:
(\frac{1}{2})^x<\frac{1}{2} nebo (\frac{1}{2})^x>4. - Nerovnice vyřešíme porovnáním exponentů:
x>1 nebo x<-2. - Množinu kořenů určíme s pomocí číselné osy: K=(-\infty,-2)\cup(1,+\infty).
Zápis řešení: