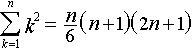|
Věta: Každá posloupnost má nejvýše jednu limitu. |
Důkaz: sporem
Pro
spor budeme předpokládat, že existuje posloupnost ![]() ,
která má dvě různé limity, tedy
,
která má dvě různé limity, tedy
lim an
= A a lim
an
= B , kde A![]() B.
B.
Dále budeme předpokládat, že A<B.
Z definice víme, že
![]()
![]()
Oba
tyto výroky musí platit pro všechna ![]() , tedy i pro
, tedy i pro ![]()
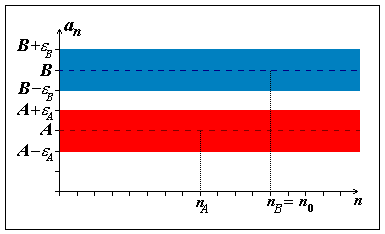
Položíme-li
n0=max(nA,nB),
pak tedy pro všechna n![]() n0
musí an
"ležet" zárověň v červeném i modrém pásu.
n0
musí an
"ležet" zárověň v červeném i modrém pásu.
|
Věta: Každá konvergentní posloupnost je omezená. |
Důkaz:
Předpokládejme,
že existuje posloupnost ![]() je konvergentní a platí
je konvergentní a platí
lim an = A
Potom potom z definice plyne
![]()
Z čísel ai , kde i =1...n0-1 najdeme minimum a označíme ho d, potom z nich najdeme maximum a označíme ho h.
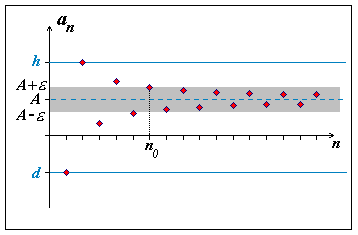
Potom bude pro každé přirozené n platit
an
= min(A
- ![]() , d)
a zároveň an
= max(A
-
, d)
a zároveň an
= max(A
- ![]() ,
h)
,
h)
|
Věta:
|
Důkaz: z definice
![]()
Chceme
tedy ukázat, že k libovolnému ![]() najdeme takové n0,
že pro všechny členy posloupnosti an
=1/n
, n0-tým
členem počínaje bude platit
najdeme takové n0,
že pro všechny členy posloupnosti an
=1/n
, n0-tým
členem počínaje bude platit
|1/n
- 0| < ![]()
1/n
< ![]()
n
< 1/![]() , tedy pro dané vždy najdeme takové n0
a to například n0
= 1/
, tedy pro dané vždy najdeme takové n0
a to například n0
= 1/![]() + 1
+ 1
Druhý vztah se dokáže podobně.
|
Věta: Nechť (an) a (bn) jsou konvergentní posloupnosti a nechť lim an = A a lim bn = B, nechť c libovolné reálné číslo. Potom jsou konvergentní i posloupnosti (an + bn), (an - bn), (an. bn), (c.an) a platí
lim (an + bn) = lim an + lim bn = A + B lim (an - bn) = lim an - lim bn = A - B lim (an . bn) = lim an . lim bn = A . B lim (c . an) = c . lim an = c . A
|
Důkaz: z definice
(an) a (bn) jsou konvergentní posloupnosti a lim an = A a lim bn = B, z definice tedy plyne
![]()
![]()
![]() > 0 je dáno, položme n0=max(nA,nB)
a
> 0 je dáno, položme n0=max(nA,nB)
a ![]() A
=
A
= ![]() B
=
B
= ![]() /2
/2
1.
| (an + bn) - (A + B)| = | an - A + bn - B |
![]() | an - A | + | bn - B |
<
| an - A | + | bn - B |
< ![]() A +
A + ![]() B
=
B
= ![]()
2.
| (an -
bn) - (A - B)| = | an - A + (B - bn) |
![]() | an - A | + | bn - B |
<
| an - A | + | bn - B |
< ![]() A +
A + ![]() B
=
B
= ![]()
3. posloupnost an je konvergentní, tady je omezená => |an| < K
položme
![]() A
=
A
= ![]() /2K
a
/2K
a
![]() B
=
B
= ![]() /2|B|
/2|B|
| (anbn) - (AB)|
= | anbn - anB
+ anB - AB | = | an(bn - B)
+ B(an - A) |
![]() | an(bn - B) |
+ | B(an - A) | = | an|.|(bn - B)|
+ |B|.|(an - A) |
<
| an(bn - B) |
+ | B(an - A) | = | an|.|(bn - B)|
+ |B|.|(an - A) |
< ![]() A +
A + ![]() B =
B = ![]()
4.
položme ![]() A
=
A
= ![]() /|c|
/|c|
| can - cA
| = |c|.| an - A |
< c.![]() A =
A = ![]()
|
Věta:
Každá geometrická posloupnost |
Důkaz:
1. q = 0 ------> an = 0 ------> lim an = 0
2.
q ![]() 0
------>
an
= a1 qn
- 1
0
------>
an
= a1 qn
- 1
------> lim an = lim a1 qn - 1 = lim a1 1/q . lim qn = a1 1/q . 0 = 0
|
Věta:
Nechť an = a1 + (n - 1) d |
Důkaz: matematickou indukcí
1. n = 1 ------> a1 = a1 + (1 - 1) d
1. n = k ------> ak = a1 + (k - 1) d
ak+1 = a1 + (k + 1 - 1) d
ak+1 = a1 + kd ------> k tomuto chceme dospět
--------------------------------------------------
------> z definice: ak+1= ak + d
------> induk. před: ak+1= a1 + (k - 1) d + d = a1 + kd
|
Věta:
Nechť
|
Důkaz:
sn = a1 + a2 + a3 + ... + an
tento součet si přepíšeme dvěma způsoby ...
sn = a1 + (a1+ d) + (a1+ 2d) + (a1+ 3d) + ... + (a1+ (n - 1)d)
sn = (a1+ (n - 1)d) + (a1+ (n - 2)d) + (a1+ (n - 3)d) + ... + (a1+ d) + a1
... a oba řádky sečteme ...
2sn = (2a1+ (n - 1)d) + (2a1+ (n - 1)d) + ... + (2a1+ (n - 1)d)
... a už jen upravit ...
2sn = n(a1+ a1+ (n - 1)d) = n(a1 + an)
![]()
|
Věta:
Nechť an = a1 qn - 1 |
Důkaz: matematickou indukcí
1. n = 1 ------> a1 = a1 q1 - 1
1. n = k ------> ak = a1 qk - 1
ak+1 = a1 qk +1 - 1
ak+1 = a1 qk ------> k tomuto chceme dospět
--------------------------------------------------
------> z definice: ak+1= ak q
------> induk. před: ak+1= a1 qk - 1 q = a1 qk
|
Věta:
Nechť sn = n an pokud q = 1
|
Důkaz:
1. q = 1
sn = a1 + a1 + a1 + ... + a1= n a1
2.
q ![]() 1
1
sn = a1 + a2 + a3 + ... + an
tento součet si přepíšeme pomocí vztahu k-tého a prvního členu ...
sn = a1 + (a1 q) + (a1 q2) + (a1 q3) + ... + (a1 qn-1)
... rovnost vynásobíme q ...
sn q = (a1 q) + (a1 q2) + (a1 q3) + ... + (a1 qn-1) + (a1 qn)
... a oba řádky od sebe odečteme ...
sn - sn q = a1 - (a1 qn)
... a už jen upravit ...
sn (1 - q) = a1 (1 - qn)
![]()
|
Věta:
Nechť Nechť (sn) je posloupnost částečných součtů. Potom je (sn) konvergentní a platí
|
Důkaz:
![]()
|q| < 1 ---------> (qn) je konvergentní a lim qn = 0
Jak bude tedy vypadat limita posloupnosti (sn) ...
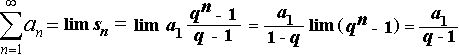
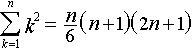
|
Odvození:
Ze znalosti vzorce (a + b)3 = a3 + 3a2b + 3ab2 + b3 víme ...
(n + 1)3 = n3 + 3n2 + 3n + 1
n3 = (n - 1)3 + 3(n - 1)2 + 3(n - 1) + 1
(n - 1)3 = (n - 2)3 + 3(n - 2)2 + 3(n - 2) + 1
...
23 = 13 + 3.12 + 3.1 + 1
... všechny tyto rovnosti sečteme ...
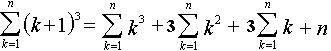
... a postupně upravíme pomocí již známých vzorců ...
![]()