2. Základní pojmy / Isomorfismus
Podle definice je graf zadán svými vrcholy (množina V) a hranami (množina E).
Pokud ale budeme konkrétní situaci popisovat pomocí grafů, může se nám stát, že dva grafy odpovídající téže situaci budou mít různě označené vrcholy a například v obrázku umístíme jednotlivé vrcholy jiným způsobem.
Například v úloze o kamarádech z úvodu použijeme pro označení vrcholů jednou první písmena křestních jmen a podruhé kamarády očíslujeme. Grafy jsou na první pohled různé - stále ale popisují stejnou situaci (kamarádi jsou stále ti samí). V takovém případě říkáme, že dané dva grafy jsou isomorfní.
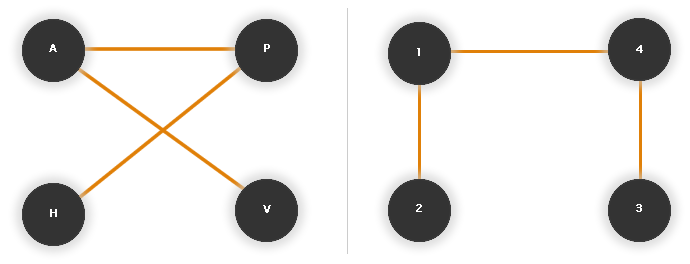
Obr. č. 2.8 - Isomorfní grafy
Zda jsou grafy isomorfní můžeme ověřit tak, že najdeme způsob, jak by se musely vrcholy prvního grafu přejmenovat, aby odpovídaly vrcholům druhého grafu - přejmenujeme-li vrcholy A a B na 1 a 2, musí být 1 a 2 spojeny hranou, pokud byly A a B spojeny hranou (a samozřejmě 1 a 2 nesmí být spojeny, pokud A a B nebyly spojeny hranou).
Takovému "přejmenování" pak říkáme bijektivní zobrazení. Bijektivní je synonymum pro vzájemně jednoznačné - každý vrchol se zobrazuje na právě jeden (dva původní vrcholy se nikdy nezobrazí na jeden nový, ani jeden původní na víc nových).
Příklad takového přejmenování pro grafy z obr. 6 by bylo: A→1, H→3, P→4, V→2.
Definice
Dva grafy G=(V,E) a G'=(V',E') nazýváme isomorfní, jestliže existuje bijektivní (vzájemně jednoznačné) zobrazení ƒ : V → V' tak, že platí:
{x,y} 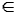 E, právě když {ƒ(x), ƒ(y)}
E, právě když {ƒ(x), ƒ(y)} 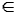 E'.
E'.
Příklad
Ukažme, že následující grafy jsou isomorfní:
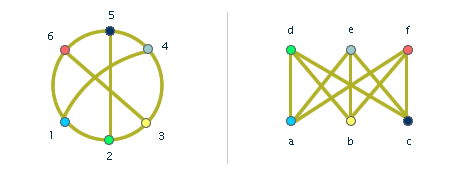
Obr. č. 2.9 - Isomorfní grafy
Hledaným isomorfismem je například zobrazení: a→1, b→3, c→5, d→2, e→4, f→6.