Stejnolehlost

Této metody používáme k řešení těch konstrukčních úloh, v nichž lze určit mezi útvarem daným a hledaným vztah stejnolehlosti. Zejména ji ale užíváme při řešení těch konstrukčních úloh, u nichž je možno podmínky, které má hledaný geometrický útvar splňovat, rozdělit na dvě části: první skupina podmínek určuje tvar, druhá určuje velikost a polohu hledaného obrazce. V tomto případě sestrojíme nejprve pomocný geometrický útvar splňující jen všechny podmínky první skupiny a určíme střed stejnolelosti, která tento útvar převede na útvar hledaný. V této stejnolehlosti pak sestrojíme útvar vyhovující i podmínkám druhé skupiny. Takto postupujeme například při sestrojování trojúhelníku, je-li jeden z daných prvků úsečka dané velikosti a ostatní prvky jsou úhly dané velikosti nebo poměr velikostí jeho stran nebo příček. Další použití stejnolehlosti je například při sestrojení obrazce, který má obsahovat daný bod nebo jehož strany mají ležet na rovnoběžce s danou přímkou.

Příklad 4

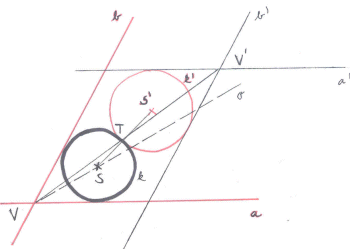
Zadání: Jsou dány dvě různoběžky a, b a kružnice k′(S′;r′), která se nedotýká žádné z obou různoběžek. Sestrojte kružnici k tak, aby se dotýkala přímek a, b a kružnice k′.

Řešení:

Rozbor: Daná úloha je polohová s jedním neznámým bodem S. Víme, že každé dvě kružnice jsou stejnolehlé, a proto i hledaná kružnice k a zadaná kružnice k′. A navíc střed stejnolehlosti u dvou kružnice, které se dotýkají, je v jejich místě dotyku. Tento bod označíme T. V této stejnolehlosti odpovídá tečně a kružnice k tečna a′  a kružnice k′, tečně b kružnice k tečna b′  b kružnice k′ a průsečíku V přímek a, b průsečík V′ přímek a′, b′. Protože vzor, obraz a střed stejnolehlosti leží ve stejnolehlosti na jedné přímce, tak přímka VV′ protíná kružnici k′ v bodě T, který je bodem dotyku obou kružnic. Střed S kružnice k pak musí ležet na přímce S′T a na ose úhlu vymezeného přímkami a a b, ve kterém leží bod T.

Řešení v AutoCADu:   

Zkouška:Z konstrukce vyplývá, že a′  a a b′  b jsou tečnami kružnice k′. Ve stejnolehlosti určené středem T a párem odpovídajících si bodů [V,V′] odpovídá tečně a′ přímka a a tečně b′ přímka b, a proto se kružnice k dotýká přímek a, b. Střed stejnolehlosti leží na kružnici k′, proto mají kružnice k a k′ v tomto místě dotyk. Kružnice k tedy splňuje všechny požadavky úlohy.

Diskuse: Protože ke kružnici k′ lze vždy sestrojit dvě tečny rovnoběžné s přímkou a, a dvě tečny rovnoběžné s přímkou b, tak existují čtyři průsečíky V′ ≠ V, které jsou vrcholy rovnoběžníka opsaného kružnici k′. Každá z přímek V′V protíná kružnici k buď ve dvou bodech, nebo v bodě žádném. Může tedy vzniknout až osm bodů T. Úloha má tedy maximálně osm řešení.

Příklad 5

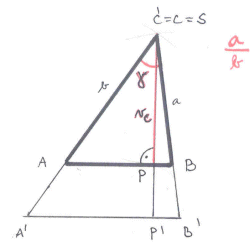
Zadání: Sestrojte trojúhelník ABC, je-li dána velikost jednoho vnitřního úhlu, poměr velikostí stran svírající tento úhel (a/b = m/n ) a velikost výšky příslušné k vrcholu tohoto úhlu.

Řešení:

Rozbor: Označme γ danou velikost úhlu, ^a/_b = ^m/_n daný poměr velikostí stran a v_c danou velikost výšky. Snadno můžeme sestrojit takový trojúhelník A′B′C′, že |A′C′| = n, |B′C′| = m, |A′C′B′| = γ, a v něm výšku C′P′ délky |C′P′| = v_c′. Pokud by bylo v_c = v_c′, pak by ΔA′B′C′ = ΔABC, čímž by úloha byla vyřešena. Je-li v_c ≠ v_c′, vyhovuje ale ΔA′B′C′ jen prvním dvěma podmínkám úlohy. V tomto případě sestrojíme ΔABC jako takový obraz ΔA′B′C′ ve stejnolehlosti se středem S = C′ = C, že výška ΔABC příslušná k vrcholu C má velikost |CP| = v_c.

Řešení v AutoCADu:    

Zkouška: Z rozboru plyne, že sestrojený trojúhelník ABC splňuje všechny dané vlastnosti.

Diskuse: Pokud γ < 180°, jsou všechny části konstrukce jednoznačné, úloha pak má jediné řešení.

Příklad 6

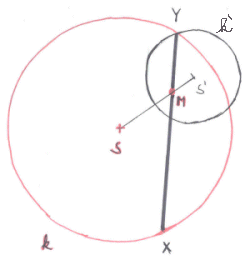
Zadání: Je dána kružnice k(S;r) a bod M v její vnitřní oblasti. Sestrojte všechny tětivy kružnice k, které procházejí bodem M a jsou jím děleny na dvě úsečky v poměru 2:5.

Řešení:

Rozbor: Úloha je zobecněním úlohy o půlení příčky v útvaru jeho daným bodem. Označme hledanou tětivu XY tak, že |MY| = ²/₅ • |MX|. Bod Y leží na polopřímce opačné k polopřímce MX, je tedy obrazem bodu X ve stejnolehlosti H(M;-0,4). Bod X  k, proto Y jako jeho obraz leží na kružnici k′(S′;0,4r), která je obrazem kružnice k v uvažované stejnolehlosti.

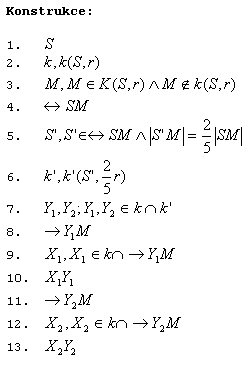
Řešení v AutoCADu:    

Zkouška: Ověříme, že úsečka XY sestrojená podle konstrukce má požadované vlastnosti, tj. X  k, Y  k, M  XY, |MY| : |MX| = 2 : 5. Y  k  k′, tedy Y  k, Y  k′, Y  k′ → X  k, M  XY, |MY| = 0,4 • |MX|. Sestrojená úsečka tedy splňuje požadované vlastnosti.

Diskuse: V daném případě má úloha dvě řešení.

Příklad 7

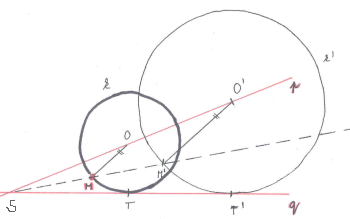
Zadání: Nechť jsou dány dvě různoběžné přímky p, q a bod M, který neleží na žádné z nich. Sestrojte kružnici, která má střed na přímce p, dotýká se přímky q a prochází bodem M.

Řešení:

Rozbor: Předpokládejme, že existuje hledaná kružnice k se středem O  p, procházející bodem M a dotýkající se přímky q v bodě T. Zvolíme-li libovolnou kružnici k′ se středem O′  p a dotýkající se přímky q v nějakém bodě dotyku T ′, pak jsou kružnice k, k′ stejnolehlé ve stejnolehlosti se středem S, jímž je průsečík přímek p, q. Obrazem bodu M  k v této stejnolehlosti je bod M′  k′, který je průsečíkem přímky SM s kružnicí k′. Stejnolehlé přímky OM a O′M′ jsou rovnoběžné.

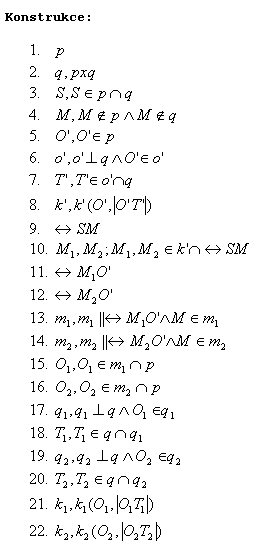
Řešení v AutoCADu:   

Zkouška: Z rozboru vyplývá, že sestrojené kružnice splňují všechny požadavky.

Diskuse: Úloha je řešitelná, právě když přímka q leží v polorovině pM, a má pak dvě řešení.