Víme už, co je to mocnina s přirozeným mocnitelem a jaká pravidla pro ni platí. Co se ale stane, když za mocnitele dosadíme celé číslo?
Nejdříve se znovu podíváme na pravidla pro počítání s mocninami s přirozeným mocnitelem. Když si jednotlivé věty pečlivě pročteme, zjistíme, že ve všech může být mocnitelem libovolné přirozené číslo.
Jenom v jedné větě je pro mocnitele připojena další podmínka. O kterou větu se jedná? Přeci o pravidlo
dělení mocnin se stejným základem! K této větě je připojena podmínka,
že pro mocnitele
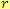
,

platí:

.
Zkusme se podívat, co se stane, když tato podmínka nebude platit. Tedy když

nebo

.
Je zřejmé, že rovnost
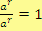
platí pro každé nenulové reálné číslo
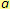
a pro libovolné přirozené číslo
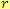
.
Využijeme-li navíc vztah
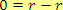
, pak můžeme psát:
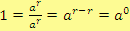
.
Proto definujeme:
Pozn. Požadujeme, aby číslo
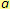
bylo nenulové, protože výraz
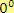
není definován.
Z tohoto zápisu je ale vidět, že námi zkoumaná věta
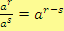
platí i v případě, že

.
2. případ:  [nahoru]
[nahoru]
Pro každé nenulové reálné číslo
a pro všechna přirozená čísla
,

, která splňují druhý případ, tedy

platí, že:

, kde

je přirozené číslo.
Odtud tedy definujeme:
Podle uvedené definice můžeme napsat následující rovnost:
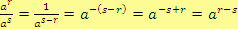
, přičemž

je záporné celé číslo. Pak ale vidíme, že věta
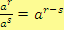
platí i v případě, že

.
Příklad[nahoru]
Vypočítej:
a)
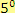 Řešení
Řešení
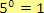
(podle definice)
b)
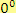 Řešení
Řešení
Tento výraz není definován.
c)
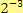 Řešení
Řešení
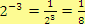
d)
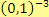 Řešení
Řešení
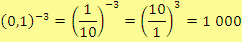
A nyní si můžeme uvést všechny věty pro počítání s mocninami s celým mocnitelem. Pozorný čtenář si jistě všimne, že tyto věty odpovídají větám pro počítání s mocninami s přirozeným mocnitelem.
Pouze zmizela podmínka pro mocnitele ve větě o dělení mocnin se stejným základem.
Příklad[nahoru]
Vypočítej za předpokladu, že
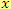
,
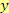
,

jsou nenulová reálná čísla:
a)
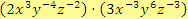 Řešení
Řešení
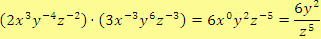
b)
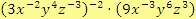 Řešení
Řešení
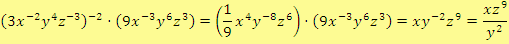
c)
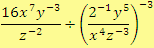 Řešení
Řešení
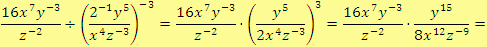
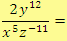
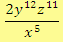
Na závěr si ještě uvedeme způsob, jakým v matematice i v dalších přírodních vědách zapisujeme velká čísla, aby byl zápis přehlednější.
Využíváme k tomu mocniny se základem 10, tedy zápis vypadá takto:

, kde
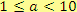
,
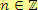
.
Exponent
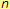
odpovídá řádu první platné číslici zapisovaného čísla.
Poznámka: Tento typ zápisu se nazývá
semilogaritmický tvar.
