Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Určování hodnot goniometrických funkcí
V následující tabulce shrneme hodnoty goniometrických funkcí pro velikosti některých úhlů.
Tabulka
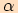 |
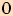 |
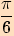 |
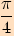 |
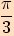 |
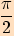 |
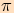 |
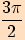 |
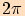 |
|---|---|---|---|---|---|---|---|---|
sinus 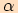 |
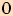 |
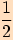 |
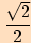 |
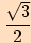 |
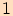 |
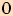 |
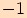 |
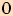 |
kosinus 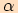 |
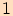 |
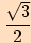 |
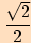 |
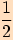 |
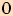 |
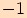 |
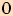 |
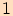 |
tangens 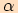 |
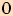 |
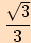 |
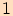 |
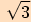 |
není definováno |
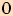 |
není definováno |
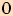 |
kotangens 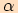 |
není definováno |
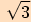 |
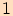 |
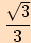 |
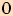 |
není definováno |
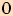 |
není definováno |
Funkční hodnoty pro úhly o velikostech 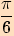 ,
,
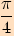 ,
,
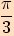 jsou odvozeny v kapitole Goniometrické funkce ostrého úhlu.
Funkční hodnoty pro
jsou odvozeny v kapitole Goniometrické funkce ostrého úhlu.
Funkční hodnoty pro 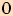 ,
,
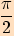 určíme buď z
jednotkové kružnice, nebo z grafu příslušné goniometrické funkce.
Hodnoty v tabulce, které nejsou z intervalu
určíme buď z
jednotkové kružnice, nebo z grafu příslušné goniometrické funkce.
Hodnoty v tabulce, které nejsou z intervalu 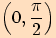 , a to
hodnoty
, a to
hodnoty 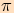 ,
, 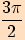 a
a 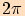 , určíme
také z jednotkové kružnice nebo z grafu funkce.
, určíme
také z jednotkové kružnice nebo z grafu funkce.
Jednotková kružnice s vyznačenými goniometrickými funkcemi
Funkční hodnoty pro další velikosti úhlů vypočítáme následujícími postupy, jejichž vysvětlení rozdělíme na 3 části.
Poznámka. V této kapitole budeme uvažovat ve stejném smyslu body a velikosti úhlů.
1. část Pro výpočet funkčních hodnot pro úhly o velikostech  využijeme sudosti,
případně lichosti funkcí.
využijeme sudosti,
případně lichosti funkcí.
Připomínáme, že funkce kosinus je funkce sudá a funkce sinus, tangens
a kotangens jsou funkce liché, tj.
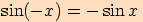
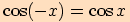
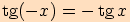
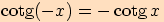
Jestliže tyto vztahy využijeme ve výpočtu, převedeme určení hodnot funkcí
sinus, kosinus, tangens a kotangens v bodech  na určení hodnot
v bodech
na určení hodnot
v bodech  .
.
Graf funkce sinus
Graf funkce kosinus
Graf funkce tangens
Graf funkce kotangens
Příklady
1.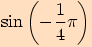

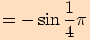

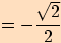

2.
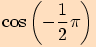

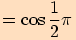

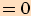

3.
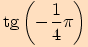

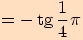

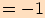

4.
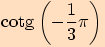

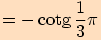

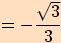

>>nahoru<<
2. část Pro úhly o velikostech
 ,
neboli
,
neboli 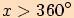 , použijeme jinou vlastnost goniometrických funkcí,
a to jejich periodičnost.
, použijeme jinou vlastnost goniometrických funkcí,
a to jejich periodičnost.
Funkce sinus a kosinus, jak víme, mají nejmenší periodu 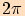 a funkce tangens a kotangens
mají nejmenší periodu
a funkce tangens a kotangens
mají nejmenší periodu 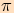 .
.
Využití této informace uvidíme na následujících příkladech.
Příklady
5.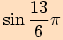

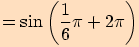

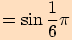

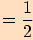

6.
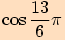

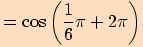

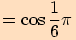

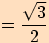

7.
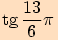

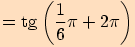

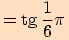

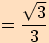

8.
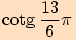

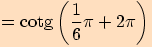

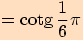

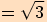

9.
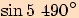

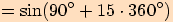

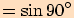

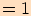

10.
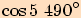

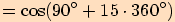



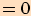

11.
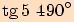



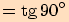
 Není definováno
Není definováno

12.
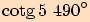

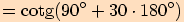



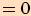

>>nahoru<<
3. část Pro úhly, jejichž velikost je z intervalů 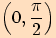 ,
,
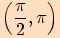 ,
, 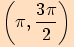 ,
,
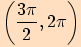 u funkcí sinus a kosinus a z intervalů
u funkcí sinus a kosinus a z intervalů 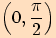 ,
,
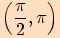 u funkcí tangens a kotangens, je postup řešení následující:
u funkcí tangens a kotangens, je postup řešení následující:
Nejprve určíme znaménko funkční hodnoty 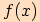 příslušné goniometrické
funkce podle intervalu, ve kterém se příslušný bod nalézá. Tedy určíme kvadrant,
v němž leží bod
příslušné goniometrické
funkce podle intervalu, ve kterém se příslušný bod nalézá. Tedy určíme kvadrant,
v němž leží bod  jednotkové kružnice
jednotkové kružnice
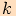 (viz tvorba jednotkové kružnice a hledání bodu
(viz tvorba jednotkové kružnice a hledání bodu 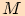 z kapitoly
Sinus a kosinus).
z kapitoly
Sinus a kosinus).
Pro přehlednost uvádíme znaménka v následující tabulce.
Tabulka
| Kvadrant | I. | II. | III. | IV. |
|---|---|---|---|---|
| Interval argumentu  |
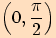 |
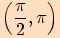 |
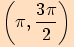 |
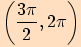 |
| sinus | + | + | - | - |
| kosinus | + | - | - | + |
| tangens | + | - | + | - |
| kotangens | + | - | + | - |
Poté, co vyhledáme příslušné znaménko v tabulce , vyjádříme uvažovanou hodnotu
argumentu  v některém z následujících tvarů,
kde
v některém z následujících tvarů,
kde 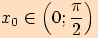 :
:
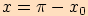 , je-li
, je-li 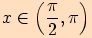 ,
tj. leží-li bod
,
tj. leží-li bod 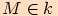 v II. kvadrantu
v II. kvadrantu
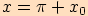 , je-li
, je-li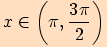 ,
tj. leží-li bod
,
tj. leží-li bod 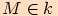 v III. kvadrantu
v III. kvadrantu
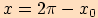 , je-li
, je-li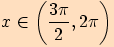 ,
tj. leží-li bod
,
tj. leží-li bod 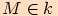 v IV. kvadrantu
v IV. kvadrantu
Pro kteroukoliv goniometrickou funkci 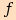 platí rovnosti
platí rovnosti 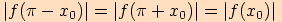 pro každé
pro každé 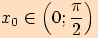 .
To lze snadno vyčíst z jednotkové kružnice nebo z grafů funkcí. Díky těmto
vztahům určíme absolutní hodnotu hledané funkční hodnoty
.
To lze snadno vyčíst z jednotkové kružnice nebo z grafů funkcí. Díky těmto
vztahům určíme absolutní hodnotu hledané funkční hodnoty 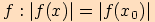 .
Tím je ovšem až na znaménko určena i hodnota
.
Tím je ovšem až na znaménko určena i hodnota 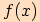 .
.
Celý postup si ukážeme a procvičíme na následujících příkladech.
Řešěný příklad
Určete funkční hodnotu sinu, kosinu, tangensu a kotangensu v bodě
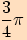 .
.
Řešení
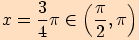 , to znamená, že bod
, to znamená, že bod
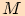 leží ve II. kvadrantu.
leží ve II. kvadrantu.
Využijeme tedy, že platí 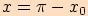 , kde
, kde
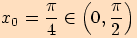 . Znaménka u jednotlivých funkčních hodnot nalezneme
v tabulce (nebo je vyčteme z jednotkové kružnice) a dále použijeme rovnost
. Znaménka u jednotlivých funkčních hodnot nalezneme
v tabulce (nebo je vyčteme z jednotkové kružnice) a dále použijeme rovnost
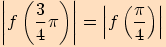 .
.
Nyní už vyjádříme postupně jednotlivé funkční hodnoty.
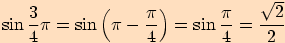
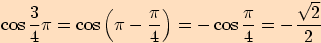
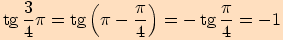
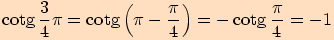

13.
Určete hodnoty goniometrických funkcí pro úhel o velikosti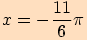 .
.

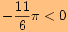 a proto využijeme sudosti funkce kosinus a lichostí ostatních funkcí.
a proto využijeme sudosti funkce kosinus a lichostí ostatních funkcí.Nyní
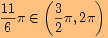 , vyjádříme
, vyjádříme
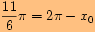 , kde
, kde
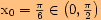
a pro funkční hodnoty platí
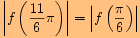 .
. 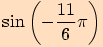

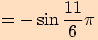

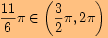
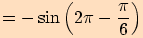

 .
.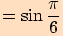

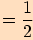

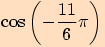

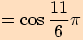

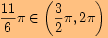
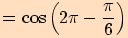

 .
.

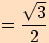

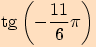

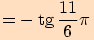

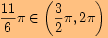
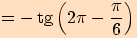

 .
.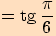

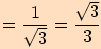

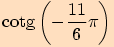

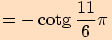

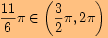
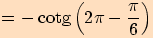

 .
.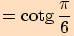

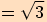

Nakonec této kapitoly ješte uvádíme applety k výpočtu funkčních hodnot goniometrických funkcí. Zde jsou uvedeny applety, které počítají funkční hodoty v radiánech. Obdobné applety, které počítají totéž ovšem ve stupních, najdete v kapitole Goniometrické funkce ostrého úhlu.
Výpočet velikosí úhlů a určení funkčních honot u goniometrických funkcí
>>nahoru<<